One type of problem is to generate a polynomial from given zeros. This can be solved using the property that if
We assume that the problem statement is as follows: We are given some zeros. If it is not specified what the multiplicity of the zeros are, we want the zeros to have multiplicity one. There are no other zeros, i.e. if a number is not mentioned in the problem statement, it cannot be a zero of the polynomial we find.
Degree of the Polynomial
Remember that the degree of a polynomial, the highest exponent, dictates the maximum number of roots it can have. Thus, the degree of a polynomial with a given number of roots is equal to or greater than the number of roots that are given. If we already count multiplicity in this number, than the degree equals the number of roots. For example, if we are given two zeros, then a polynomial of second degree needs to be constructed.
Solution and Constants
If
This already gives us the solution of our problem: an answer to our question is just the product of all factors
For any nonzero constant
Thus if we find a solution
Thus for given zeros
For example, if given
Multiplied out, this gives:
Example
Given zeros
In the picture below, the blue graph represents the solution for
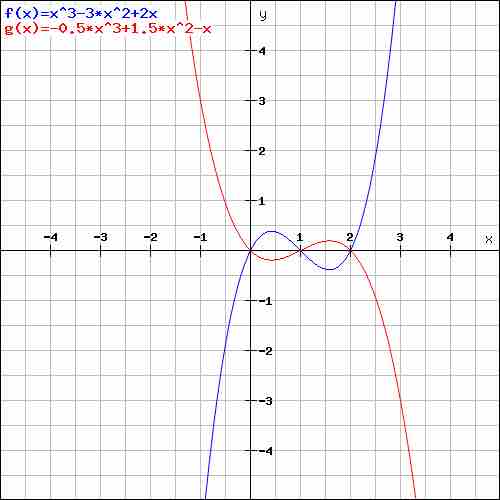
Example
Two polynomials with the same zeros: Both