The factored form of a polynomial can reveal where the function crosses the $x$-axis. An $x$ -value at which this occurs is called a "zero" or "root. "

Number of Zeros of a Polynomial

Consider the factored function:

$f(x)=(x-a_1)(x-a_2)...(x-a_n)$

Each value $a_1,a_2$, and so on is a zero.

A polynomial function may have many, one, or no zeros. All polynomial functions of positive, odd order have at least one zero (this follows from the fundamental theorem of algebra), while polynomial functions of positive, even order may not have a zero (for example $x^4+1$ has no real zero, although it does have complex ones).

Regardless of odd or even, any polynomial of positive order can have a maximum number of zeros equal to its order. For example, a cubic function can have as many as three zeros, but no more. This is known as the fundamental theorem of algebra.

Example

Consider the function

$f(x)=x^3+2x^2-5x-6$

This can be rewritten in factored form:

$f(x)=(x+3)(x+1)(x-2)$

Replacing $x$ with a value that will make either $(x+3),(x+1)$  or $(x-2)$ zero will result in $f(x)$ being equal to zero. Thus, the zeros for $f(x)$ are at $x=-3,x=-1$ and $x=2.$ This can also be shown graphically:

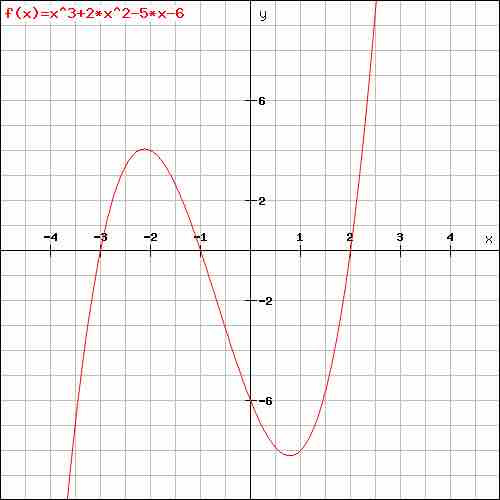
Cubic function

Graph of the cubic function $f(x) = x^3 + 2x^2 - 5x - 6 = (x+3)(x+1)(x-2).$ We see that its roots equal the negative second coefficients of its first degree factors.

Factoring and zeros

In general, we know from the remainder theorem that $a$ is a zero of $f(x)$ if and only if $x-a$ divides $f(x).$ Thus if we can factor $f(x)$ in polynomials of as small a degree as possible, we know its zeros by looking at all linear terms in the factorization. This is why factorization is so important: to be able to recognize the zeros of a polynomial quickly.

It follows from the fundamental theorem of algebra and a fact called the complex conjugate root theorem, that every polynomial with real coefficients can be factorized into linear polynomials and quadratic polynomials without real roots. Thus if you have found such a factorization of a given function, you can be completely sure what the zeros of that function are.