What is a Linear Function?
A linear function is an algebraic equation in which each term is either a constant or the product of a constant and (the first power of) a single variable. For example, a common equation,
Graphs of Linear Functions
The origin of the name "linear" comes from the fact that the set of solutions of such an equation forms a straight line in the plane. In the linear function graphs below, the constant,
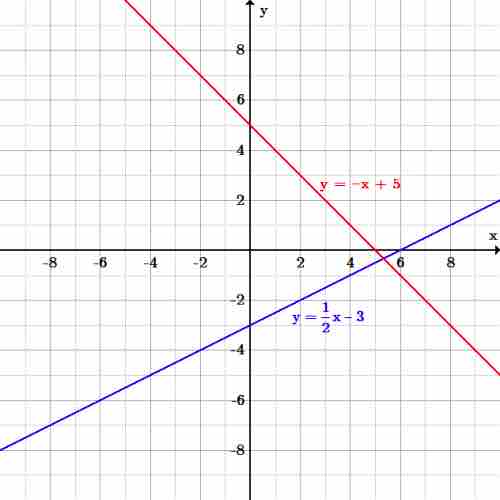
Graphs of linear functions
The blue line,
Vertical and Horizontal Lines
Vertical lines have an undefined slope, and cannot be represented in the form
Horizontal lines have a slope of zero and is represented by the form,