Slope

In mathematics, the slope of a line is a number that describes both the direction and the steepness of the line. Slope is often denoted by the letter $m$. Recall the slop-intercept form of a line, $y = mx + b$. Putting the equation of a line into this form gives you the slope ($m$) of a line, and its $y$-intercept ($b$). We will now discuss the interpretation of $m$, and how to calculate $m$ for a given line.

The direction of a line is either increasing, decreasing, horizontal or vertical. A line is increasing if it goes up from left to right which implies that the slope is positive ($m > 0$). A line is decreasing if it goes down from left to right and the slope is negative ($m < 0$) . If a line is horizontal the slope is zero and is a constant function ($y=c$). If a line is vertical the slope is undefined.

Slopes of Lines

The slope of a line can be positive, negative, zero, or undefined.

The steepness, or incline, of a line is measured by the absolute value of the slope. A slope with a greater absolute value indicates a steeper line. In other words, a line with a slope of $-9$ is steeper than a line with a slope of $7$.

Calculating Slope

Slope is calculated by finding the ratio of the "vertical change" to the "horizontal change" between any two distinct points on a line. This ratio is represented by a quotient ("rise over run"), and gives the same number for any two distinct points on the same line. It is represented by $m = \frac{rise}{run}$.$$

Visualization of Slope

The slope of a line is calculated as "rise over run."

Mathematically, the slope m of the line is:

$\displaystyle m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ 

Two points on the line are required to find $m$. Given two points $(x_1, y_1)$ and $(x_2, y_2)$, take a look at the graph below and note how the "rise" of slope is given by the difference in the $y$-values of the two points, and the "run" is given by the difference in the $x$-values.

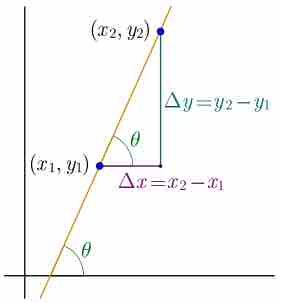
Slope Represented Graphically

The slope $m =\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ is calculated from the two points $\left( x_1,y_1 \right)$ and $\left( x_2,y_2 \right)$.

Now we’ll look at some graphs on a coordinate grid to find their slopes. In many cases, we can find slope by simply counting out the rise and the run. We start by locating two points on the line. If possible, we try to choose points with coordinates that are integers to make our calculations easier. 

Example

Find the slope of the line shown on the coordinate plane below.

Find the slope of the line

Notice the line is increasing so make sure to look for a slope that is positive. 

Locate two points on the graph, choosing points whose coordinates are integers. We will use $(0, -3)$ and $(5, 1)$. Starting with the point on the left, $(0, -3)$, sketch a right triangle, going from the first point to the second point, $(5, 1)$. 

Identify points on the line

Draw a triangle to help identify the rise and run.

Count the rise on the vertical leg of the triangle: $4$ units. 

Count the run on the horizontal leg of the triangle: $5$ units.

Use the slope formula to take the ratio of rise over run: 

$\displaystyle \begin{aligned} m &= \frac{rise}{run} \\ &= \frac{4}{5} \end{aligned}$

The slope of the line is $\frac{4}{5}$. Notice that the slope is positive since the line slants upward from left to right.

Example

Find the slope of the line shown on the coordinate plane below.

Find the slope of the line

We can see the slope is decreasing, so be sure to look for a negative slope. 

Locate two points on the graph. Look for points with coordinates that are integers. We can choose any points, but we will use $(0, 5)$ and $(3, 3)$. 

Identify two points on the line

The points $(0, 5)$ and $(3, 3)$ are on the line.

Apply the formula for slope:

 $\displaystyle m =\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

Let $(x_1, y_1)$ be the point $(0, 5)$, and $(x_2, y_2)$ be the point $(3, 3)$. 

Plugging the corresponding values into the slope formula, we get: 

$\displaystyle \begin{aligned} m &= \frac{3-5}{3-0} \\ &= \frac{-2}{3} \end{aligned}$

The slope of the line is $- \frac{2}{3}$. Notice that the slope is negative since the line slants downward from left to right.