Introduction
Just as it is possible for a variable to grow exponentially as a function of another, so can the a variable decrease exponentially. Consider the decrease of a population that occurs at a rate proportional to its value. This rate at which the population is decreasing remains constant but as the population is continually decreasing the overall decline becomes less and less steep.
Exponential rate of change can be modeled algebraically by the following formula:
where
Half Life
The time it takes for a substance (drug, radioactive nuclide, or other) to lose half of its pharmacological, physiological, biological, or radiological activity is called its half-life. The exponential decay of the substance is a time-dependent decline and a prime example of exponential decay.
As an example let us assume we have a
Use of Half Life in Carbon Dating
Half-life is very useful in determining the age of historical artifacts through a process known as carbon dating. Given a sample of carbon in an ancient, preserved piece of flesh, the age of the sample can be determined based on the percentage of radioactive carbon-13 remaining. 1.1% of carbon is C-13 and it decays to carbon-12. C-13 has a half-life of 5700 years—that is, in 5700 years, half of a sample of C-13 will have converted to C-12, which represents approximately all the remaining carbon. Using this information it is possible to determine the age of the artifact given the amount of C-13 it presently contains, and comparing it to the amount of C-13 it should contain.
Half-life can be mathematically defined as:
It can also be conveniently inserted into the exponential decay formula as follows:
Thus, if a sample is found to contain 0.55% of its carbon as C-13 (exactly half of the usual 1.1%), it can be calculated that the sample has undergone exactly one half-life, and is thus 5,700 years old.
Below is a graph highlighting exponential decay of a radioactive substance. Using the graph, find that half-life.
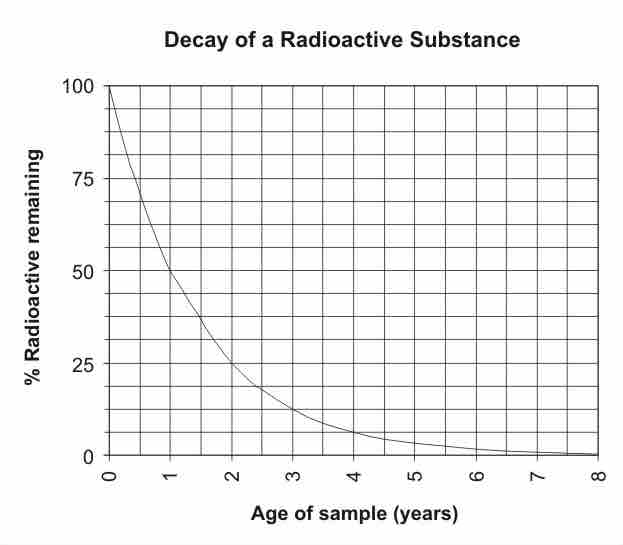
Graph depicting radioactive decay
The amount of a substance undergoing radioactive decay decreases exponentially, eventually reaching zero. Since there is 50% of the substance left after 1 year, the half-life is 1 year.