History of the Matrix
The matrix has a long history of application in solving linear equations. They were known as arrays until the
What is a Matrix
In mathematics, a matrix (plural matrices) is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. Matrices are commonly written in box brackets. The horizontal and vertical lines of entries in a matrix are called rows and columns, respectively.
The size of a matrix is defined by the number of rows and columns that it contains. A matrix with m rows and n columns is called an m × n matrix or
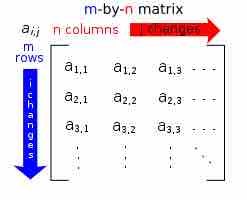
Matrix Dimensions
Each element of a matrix is often denoted by a variable with two subscripts. For instance,
The individual items (numbers, symbols or expressions) in a matrix are called its elements or entries. Provided that they are the same size (have the same number of rows and the same number of columns), two matrices can be added or subtracted element by element. The rule for matrix multiplication, however, is that two matrices can be multiplied only when the number of columns in the first equals the number of rows in the second. Any matrix can be multiplied element-wise by a scalar from its associated field.
Matrices which have a single row are called row vectors, and those which have a single column are called column vectors. A matrix which has the same number of rows and columns is called a square matrix. In some contexts, such as computer algebra programs, it is useful to consider a matrix with no rows or no columns, called an empty matrix.