Chapter 9
Matrices
By Boundless
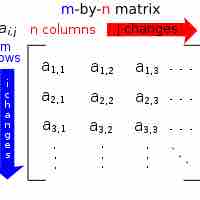
A matrix is a rectangular arrays of numbers, symbols, or expressions, arranged in rows and columns.
There are a number of operations that can be applied to modify matrices, such as matrix addition, subtraction, and scalar multiplication.

When multiplying matrices, the elements of the rows in the first matrix are multiplied with corresponding columns in the second matrix.
The identity matrix
Matrices can be used to compactly write and work with systems of multiple linear equations.
Two matrices are row equivalent if one can be changed to the other by a sequence of elementary row operations.
Using elementary operations, Gaussian elimination reduces matrices to row echelon form.
The determinant of a square matrix is computed by recursively performing the Laplace expansion to find the determinant of smaller matrices.
The cofactor of an entry
Cramer's Rule uses determinants to solve for a solution to the equation