Introduction

Fundamentally, compound interest is an application of exponential functions that is found very commonly in every day life. Interest is, generally, a fee charged for the borrowing of money. The two classic cases are (1) interest accrued as part of loan and (2) interest accrued in a savings or other account. In the first case the client owes the amount borrowed plus the interest. In the second, the bank pays the client interest for maintaining money in the account. If you are the client, you are losing money in the first case and earning money in the second.

The amount of interest accrued depends on the principal (amount borrowed/deposited), the interest rate (a percentage of the principal), period (amount of time between interest payments) and time elapsed.

For questions of interest, unless otherwise stated, the amount borrowed/deposited remains unchanged. The client does not, for example, add or withdraw funds from the savings account after the initial deposit (the principal) is made.

Simple vs. Compound Interest

There exist two kinds of interest: simple and compound. 

In simple interest, interest is accrued on the principal alone. This means that the amount of interest earned in each compounding period is the same because interest is earned based on the principal which remains unchanged.  

In compound interest, interest is accrued on both the principal and on prior interest earned. For this reason, if all other conditions are the same (principal, rate, time elapsed and frequency of interest payments) compound interest grows at a faster rate than simple interest. The amount of interest earned increases with each compounding period.

Simple Interest: An Example

Simple interest is accrued linearly based on the formula: 

$\displaystyle I=p\cdot r \cdot \frac{t}{f}$ 

Where $I$ represents the interest, $p$ is the principal, $r$ is interest rate (expressed as a decimal), $t$ is time elapsed, and $f$ is the time elapsed per interest payment. The ratio of $t$ to $f$ is often simplified to the number of interest payments. Total amount owed/earned which includes the principal and the interest is given by $A=P+I$.

Example 1: You deposit $100 into a bank account earning 5% annual interest. How much money is in the account at the end of 1, 2, 3, 4, and $n$years?

Let us begin by determining the interest at the end of the first year. We use the formula $I=p\cdot r \cdot \frac{t}{f}$ with $p=100$, $r=.05$, $t=1$ and $f=1$. The interest earned at the end of the year is: 

$\displaystyle \begin{aligned} I&=(100)(.05)(\frac{1}{1})\\& =5 \end{aligned}$

The amount in the account at the conclusion of the year is given by $100+5=105$. It is useful to note that the account will earn $$5$ in interest every single year irrespective of how long the money is in the account or what the amount in the account is during any given year. This can be seen by the fact that the amount after $n$ years is given by a linear function with slope equal to five (see table below).

The table below shows the calculations, interest earned and total amount in the account after 1, 2, 3, 4, and n years.

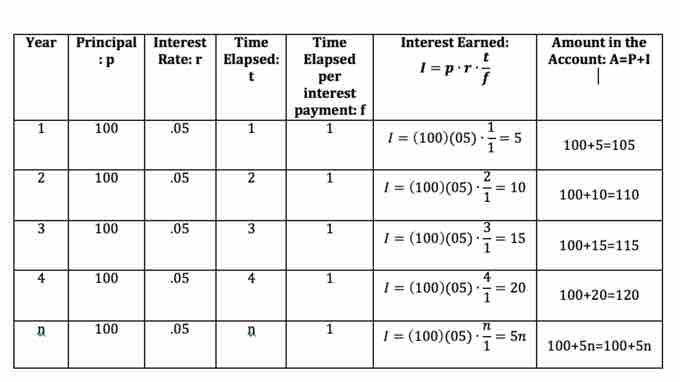
Calculations of interest earned and amount in the account for Example 1

Compound Interest: An Example

Compound interest is not linear, but exponential in form. That is, the amount of interest earned is not constant but instead changes with time based on the total amount of the amount in the account.

The equation representing investment value as a function of principal, interest rate, period and time is: 

$\displaystyle M=p(1+r)^\frac{t}{f}$ 

Where $M$ represents the total value (including principal), $p$ represents principal, $r$ is interest rate (expressed as a decimal), $t$ is time elapsed, and $f$ is the length of time between payments. To calculate interest alone, simply subtract the principal from $M$.

We now re-consider Example 1 above. This time we use compound interest instead.

Example 2: You deposit $100 into a bank account earning 5% interest compounded annually. How much money is in the account at the end of 1, 2, 3, 4, and $n$ years?

Let us begin by determining the amount in the account after the first year  using the formula $M=p(1+r)^\frac{t}{f}$ with $p=100$, $r=.05$, $t=1$ and $f=1$. The amount in the account after one year is:

$\displaystyle \begin{aligned} M&=(100)(1+.05)^\frac{1}{1}\\ &=105 \end{aligned}$  

This is the exact amount that was in the account after the first year using simple interest. That is because the difference is that compound interest earns interest on both the principal and prior interest. At the end of the first year there was no prior interest in the account. We will see differences between simple and compound interest in this, and similar problems, in the second year.

Let us determine the amount in the account after the second year again using the formula $M=p(1+r)^\frac{t}{f}$ but now letting $t=2$. We obtain:

$\displaystyle \begin{aligned} M&=100(1+.05)^\frac{2}{1}\\ &=110.25 \end{aligned}$ 

That is, there are $25$ cents more in account in the second year using compound interest instead of simple interest. This might not seem like a lot but the amount of interest earned will continue to increase each year as there is more and more money in the account. Every year the interest earned will be higher than in the previous year, whereas in simple interest the amount each year is fixed.

The following table includes the calculations, interest earned and total amount in the account at the end of $1,2,3,4$ and $n$ years.

Calculations of interest earned and amount in the account for Example 2

The amount in the account is greater each year beginning with year two when using compound interest rather than simple interest. However, because the principal is so small and the number of years elapsed only 4, it does not appear that the difference between the two example is that great. Let us consider one last problem where we let the time elapsed be much greater.

Simple vs. Compound Interest Over Time: An Example

The biggest differences between the amount of money in an account using simple versus compound interest are seen over extended periods of time. To highlight this, we return the the examples we did prior and now consider how much money is in each account after 50 years.

Example 3: You deposit $100 into a bank account earning 5% interest compounded annually. How much money is in the account at the end of 50 years? How does this compare to the amount in the account after 50 years if the interest had been compounded annually?

The money in the account using simple interest after $50$ years is given by

 $\displaystyle \begin{aligned} P+I&=100+(100)(.05)(\frac{50}{1})\\ &=350 \end{aligned}$

However, the amount in the account using compound interest after $50$ years is given by: 

$\displaystyle \begin{aligned} M&=(100)(1+.05)^\frac{50}{1}\\ &=1146.74 \end{aligned}$ 

A difference of $$796.74$.

Frequency of Compounding Periods

The more frequent the compounding periods the more interest is accrued. Therefore, if one deposits money into a bank account that earns compound interest, and does not add or withdraw any additional funds, the amount of money in the bank would increase as the number of compounding periods per year increases. You earn more interest when interest is compounded quarterly ($4$ times a year) than once a year. You earn more interest when interest is compounded monthly ($12$ times a year) than quarterly. You earn more interest when interest is compounded daily ($365$ times a year) than monthly and so on. You earn the most interest when interest is compounded continuously. 

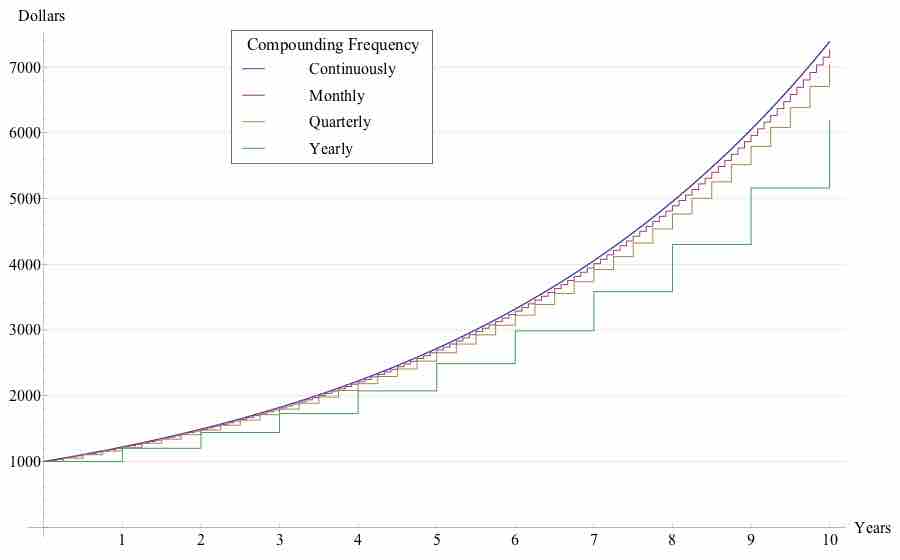
Graph of interest accrued under differing number of compounding periods per year 

Starting with a principal of $1000, interest rises exponentially. The graph shows that the more frequent the number of compounding periods the more interest is accrued and shows this visually for yearly, quarterly, monthly and continuous compounding.

Interest Compounded Continuously

Given that the more frequent the compounding periods per year, the more interest is accrued it might come as a surprise that money deposited into a bank account accrues compound interest continuously. You might expect the bank would choose a smaller number of compounding periods in order to pay out less in interest, but this is not the case. To see why let us take the following example: You deposit $$1$ in the bank in an account earning $100$% interest. You do not add or withdraw money from the account. In this situation the amount of money in the account will be given by $(1+\frac{1}{n})^n$ where $n$ is the number of compounding periods and $\frac{1}{n}$ is the rate per compounding period. This is a simplification of the prior formula used because of the specific conditions of this most recent situation. We expect that as $n$ increases the amount in the account also increases, but if the amount grows without bounds then banks would be giving away much money as they compound interest continuously. 

The following table shows the amount in the account at the end of one year when interest is compounded with differing frequencies.

Amount in account after 1 year with interest compounded at different frequencies

What we see from the table is that while the interest earned increases as the number of compounding periods increase, that the rate at which it increases is slowing down. Going from $1$ to $4$ compounding periods yields an increase of $44$ cents but going from $100$ to $1000$ barely raises the interest $1$ cent. Another way of saying this is that the amount in the account is approaching a limiting value. The numbers in the table are getting closer and closer to the number $e$. The number $e$ is used as the base of the natural logarithm and is equal to approximately $2.718281828$. No matter how long the money is in the account, it will not grow beyond that value.

The formula for compound interest with the number of compounding periods going to infinity yields the formula for compounding continuously. It should come as no surprise that this formula involves the number $e$.

The formula for the amount of money in an account where interest is compounded continuously is given by $A=Pe^{rt}$ where $P$ is the principal, $r$ is the annual rate written as a decimal and $t$ is the time in years.