Introduction
Exponential functions can be used to model growth and decay. For example, the world's human population is growing exponentially as can be seen in the following graph.
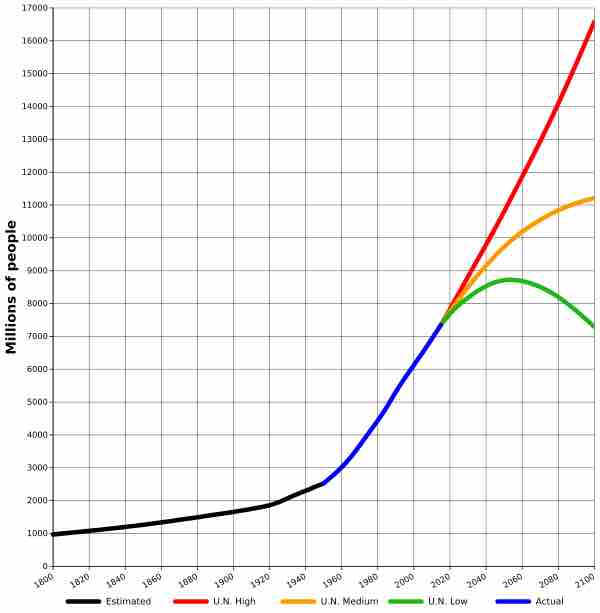
World Population from 1800 AD to 2100 AD
Three projections for the world's population are shown, with a low estimate reaching a peak and then decreasing, a medium estimate increasing but at an ever-slower rate, and a high estimate continuing to increase exponentially.
There is, however, a limit to how accurate a model such as this can be. Even if we account for varying rates of growth, the idea that human population can be modeled strictly with an exponential function is misguided. Exponential functions are ever-increasing so saying that an exponential function models population growth exactly means that the human population will grow without bound. That is not sound reasoning, as the human population is affected by various factors among these are access to resources such as food, water, and shelter. At some point in the future, the number of humans will grow so large that there will not be enough resources to sustain growth. Thus the exponential model, while perhaps useful in the short-term, is not accurate in the long-term for real world simulation. At some point the growth must level off. This is the idea behind limited growth, that a population may grow exponentially but only to a point at which time the growth will taper off.
As an alternative, consider a farm upon which a population of sheep are kept in a constant, comfortable climate in a fully enclosed field. Assume the entire system is closed from gains and losses, but for a flow of a stream of clean drinking water through the field.
With no predators, the population of sheep would perfectly fit an exponential model to a certain point when the availability of food would act as a limiting factor. If the amount of grass available to the sheep and its rate of replenishing are constant, eventually the population of sheep will grow to a tipping point at which there is no longer enough grass to feed the sheep. The death rate of sheep will increase as some starve. Thus, the model of population growth among sheep will no longer be exponential.
Logistic Growth Model
To account for limitations in growth, the logistic growth model can be used. The logistic growth model is given by
Evaluating a Logistic Growth Function
Given various conditions, it is possible to evaluate a logistic function for a particular value of
Example 1: Evaluate the logistic growth function $P(t)=\frac{50}{1+8\cdot e^{-3t}}$ for $t=6$
To evaluate this function we plug
Graphing a Logistic Growth Model
Graphically, the logistic function resembles an exponential function followed by a logarithmic function that approaches a horizontal asymptote. This horizontal asymptote represents the carrying capacity. That is,
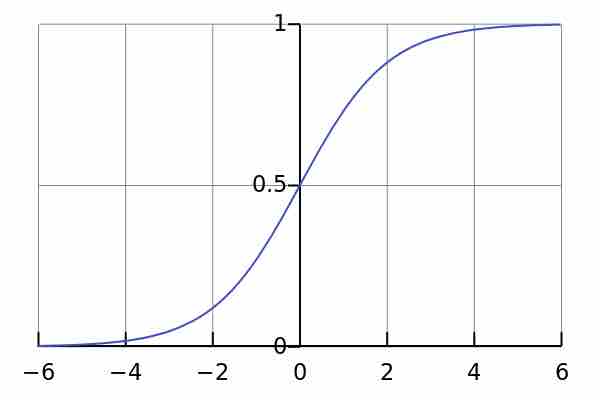
Graph of a logistic function
Logistic functions have an "s" shape, where the function starts from a certain point, increases, and then approaches an upper asymptote.