Introduction
Population growth can be modeled by an exponential equation. Namely, it is given by the formula
The rate
Population Growth Rate
The population size can fluctuate from growth to decline, and back again. As such, another variable is important when studying population demographics and dynamics. It is the Population Growth Rate (
If we multiply the
A positive growth rate indicates an increasing population size, while a negative growth rate is characteristic of a decreasing population. A growth rate of
World Population
In demographics, the world population is the total number of humans currently living. As of March 2016, it was estimated at 7.4 billion, an all-time high. The United Nations estimates it will further increase to 11.2 billion in the year 2100. If the current rates of births and deaths hold, the world population growth can be modeled using an exponential function. The graph below shows an exponential model for the growth of the world population.
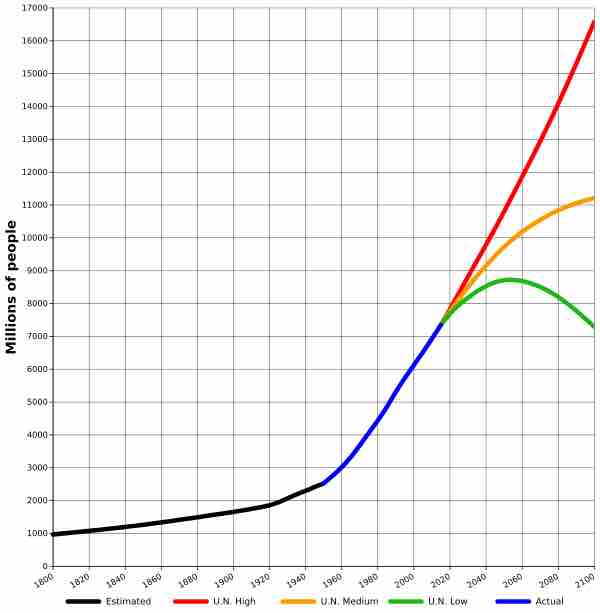
World-Population from 1800 (actual) to 2100 (projected)
The projected world population growths after the present day must be projected. A high estimation predicts the graph to continue at an increasing rate, a medium estimation predicts the population to level off, and a low estimation predicts the population to decline.
The graph has the general shape of an exponential curve though it is not exact as is the case usually when we deal with real data as opposed to purely mathematical constructs. The data is at times estimated, at times actual and at times projected. Projections for high (red), medium (orange) and low (green) rates of change are represented accounting for the splitting off of the curve after 2016.