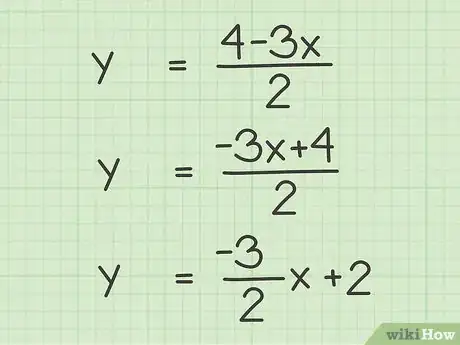How to Solve Literal Equations

Co-authored by wikiHow Staff

Last Updated: January 16, 2023 References

A literal equation is an equation that has all variables or multiple variables. To solve a literal equation, you need to solve for a determined variable by using algebra to isolate it.^{[1]
X
Research source} You will often need to do this when rearranging geometric formulas or when solving linear equations. In order to solve literal equations, use the same algebraic principles you would use to solve linear equations.

Method 1

Method 1 of 3:

Rearranging Geometric Formulas

1
Determine which variable you need to isolate. Isolating a variable means getting the variable on one side of an equation by itself. This information should be given to you, or you can figure it out based on what information you know you will be given.^{[2]
X
Research source}
- For example, you might be told to solve the area of a triangle formula for $h$ . Or, you might know that you have the area and base of the triangle, so you need to solve for the height. So, you need to rearrange the formula and isolate the $h$ variable.
2
Use algebra to solve for the desired variable. Use inverse operations to cancel variables on one side of the equation and move them to the other side. Keep in mind the following inverse operations:
- Multiplication and division.
- Addition and subtraction.
- Squaring and taking a square root.
Advertisement
3
Keep the equation balanced. Whatever you do to one side of the equation, you must also do to the other side. This ensures that your equation remains true, and in the process you are moving variables from one side to the other as needed.
- For example, to solve the area of a triangle formula ( $A={\frac {1}{2}}bh$ $A={\frac {1}{2}}bh$ ) for $h$ $h$ :
  - Cancel the fraction by multiplying each side by 2:
    $A\times 2=2\times {\frac {1}{2}}bh$
    $2A=bh$
  - Isolate $h$ by dividing each side by $b$ :
    ${\frac {2A}{b}}={\frac {bh}{b}}$
    ${\frac {2A}{b}}=h$
- Rearrange the formula, if desired: $h={\frac {2A}{b}}$

Method 2

Method 2 of 3:

Rearranging Equations of Lines

1
Remember the slope-intercept form for the equation of a line. The slope-intercept form is $y=mx+b$ , where $y$ equals the y-coordinate of a point on the line, $x$ equals the x-coordinate of that same point, $m$ equals the slope of the line, and $b$ equals the y-intercept.^{[3]
X
Research source}
2
Remember the standard form of a line. The standard form is $Ax+By=C$ , where $x$ and $y$ are the coordinates of a point on the line, $A$ is a positive integer, and $B$ and $C$ are integers.^{[4]
X
Research source}
3
Use algebra to isolate the appropriate variable. Use inverse operations to move variables from one side of the equation to the other side. Remember to keep the equation balanced, which means that whatever you do to one side of the equation, you must also do to the other side.^{[5]
X
Research source}
- For example, you might have the equation of a line $3x+2y=4$ $3x+2y=4$ . This is in standard form. If you need to find the y-intercept of the line, you need to rearrange the formula to slope-intercept form by isolating the $y$ $y$ variable:^{[6]
  X
  Research source}
  - Subtract $3x$ from both sides of the equation:
    $3x+2y-3x=4-3x$
    $2y=4-3x$ .
  - Divide both sides by $2$ :
    ${\frac {2y}{2}}={\frac {4-3x}{2}}$
    $y={\frac {4-3x}{2}}$
4
Reorder the variables and constants, if necessary. If you are changing an equation to slope-intercept or standard form, rearrange the variables, coefficients, and constants so that they follow the correct formula.^{[7]
X
Research source}
- For example, to change $y={\frac {4-3x}{2}}$ to the correct slope-intercept formula, you need to switch the order of the number in the numerator, then simplify:
  $y={\frac {-3x+4}{2}}$
  $y={\frac {-3}{2}}x+2$
  Now, since the formula is in proper slope-intercept form, it is easy to identify the y-intercept as 2.

Method 3

Method 3 of 3:

Solving Sample Problems

1
Solve this equation for $b$ . $R=5bd-6ba$ $R=5bd-6ba$ .
- Factor out the $b$ : $R=b(5d-6a)$ .
- Isolate the $b$ by dividing each side by the expression in parentheses:
  ${\frac {R}{5d-6a}}={\frac {b(5d-6a)}{5d-6a}}$
  ${\frac {R}{5d-6a}}=b$
2
Solve the circumference of a circle formula for the radius. The formula is $C=2\pi {r}$ $C=2\pi {r}$ ^{[8]
X
Research source}
- Understand what each variable stands for. In this formula, $C$ is the circumference, and $r$ is the radius. So you need to isolate the $r$ to solve for the radius.
- Isolate the $r$ by dividing both sides of the equation by $2\pi$ :
  ${\frac {C}{2\pi }}={\frac {2\pi {r}}{2\pi }}$
  ${\frac {C}{2\pi }}=r$
- If desired, reverse the order of the equation for standard form: $r={\frac {C}{2\pi }}$ .
3
Rewrite this equation of a line in standard form. $y={\frac {1}{2}}x+5$ $y={\frac {1}{2}}x+5$
- Recall that standard form is $Ax+By=C$ .
- Cancel the fraction by multiplying each side of the equation by 2:
  $2y=2({\frac {1}{2}}x+5)$
  $2y=x+10$
- Subtract $x$ from both sides of the equation:
  $2y-x=x+10-x$
  $2y-x=10$
- Rearrange the $y$ and $x$ variables so that they are in the standard form: $-x+2y=10$ .
- Multiply both sides by $-1$ , since $A$ should be a positive integer for standard form:^{[9]
  X
  Research source}
  $-1(-x+2y)=-1(10)$
  $x-2y=-10$

Community Q&A

Question

How do I solve 3x + w - r = y?

Donagan

Top Answerer

Because you're working with four variables, you would need a total of four separate equations, each containing those variables, in order to find their values.
Question

In the equation Perimeter = 2(L + W), what is L?

Donagan

Top Answerer

L is the length of whatever figure you're working with.
Question

For the equation 12am = 4, how do I solve for a?

Donagan

Top Answerer

Divide both sides of the equation by 12m.