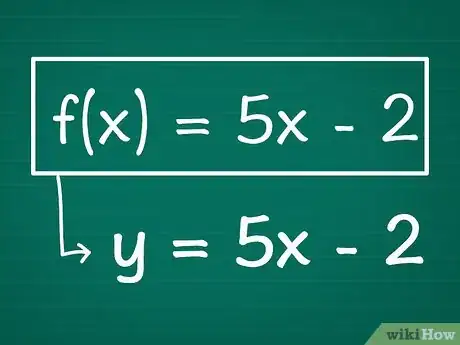wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 17 people, some anonymous, worked to edit and improve it over time.
There are 7 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 153,237 times.
Learn more...
A mathematical function (usually denoted as f(x)) can be thought of as a formula that will give you a value for y if you specify a value for x. The inverse of a function f(x) (which is written as f-1(x))is essentially the reverse: put in your y value, and you'll get your initial x value back.[1] Finding the inverse of a function may sound like a complex process, but for simple equations, all that's required is knowledge of basic algebraic operations. Read on for step-by-step instructions and an illustrative example.
Steps
-
1Write your function, replacing f(x) with y if necessary. Your formula should have y on one side of the equals sign by itself with the x terms on the other side of the equals sign. If you have an equation that's already written in terms of y and x (for instance, 2 + y = 3x2), all you need to do is solve for y by isolating it on one side of the equals sign.[2]
- Example: If we have a function f(x) = 5x - 2, we would rewrite it as y = 5x - 2 simply by replacing the "f(x)" with a y.
- Note: f(x) is the standard function notation, but if you're dealing with multiple functions, each one gets a different letter to make telling them apart easier. For example, g(x) and h(x) are each common identifiers for functions.
-
2Solve for x. In other words, perform the necessary mathematical operations to isolate x by itself on one side of the equal sign. Basic algebraic principles will guide you here: if x has a numeric coefficient, divide both sides of the equation by this number; if a certain number is added to the x term(s) on one side of the equals sign, subtract this number from both sides, and so on.[3]
- Remember, you can perform any operation on one side of the equation as long as you perform the operation on every term on both sides of the equal sign.
- Example: To continue our example, first, we'd add 2 to both sides of the equation. This gives us y + 2 = 5x. We'd then divide both sides of the equation by 5, yielding (y + 2)/5 = x. Finally, to make it easier to read, we'll rewrite the equation with "x" on the left side: x = (y + 2)/5.
Advertisement -
3Switch the variables. Replace x with y and vice versa. The resulting equation is the inverse of the original function. In other words, if we substitute a value for x into our original equation and get an answer, when we substitute that answer into the inverse equation (again for x), we'll get our original value back![4]
- Example: After switching x and y, we'd have y = (x + 2)/5
-
4Replace y with "f-1(x)." Inverse functions are usually written as f-1(x) = (x terms) . Note that in this case, the -1 exponent doesn't mean we should perform an exponent operation on our function. It's just a way of indicating that this function is the inverse of our original.[5]
- Since taking x to the -1st power gives the fraction 1/x, you can also think of f-1(x) as a way of writing "1/f(x)," which also signifies the inverse of f(x).
-
5Check your work. Try substituting a constant into the original function for x. If you found the correct inverse, you should be able to plug the result into the inverse function and get your original x-value as the result.[6]
- Example: Let's substitute 4 for x in our original equation. This gives us f(x) = 5(4) - 2, or f(x) = 18.
- Next, let's substitute our answer, 18, into our inverse function for x. If we do this, we get y = (18 + 2)/5, which simplifies to y = 20/5, which further simplifies to y = 4. 4 is our original x-value, so we know we've calculated the correct inverse function.
Community Q&A
-
QuestionWhere do I use inverse functions?
 Community AnswerFor one thing, any time you solve an equation. To solve x+4 = 7, you apply the inverse function of f(x) = x+4, that is g(x) = x-4, to both sides (x+4)-4 = 7-4 . To solve 2^x = 8, the inverse function of 2^x is log2(x), so you apply log base 2 to both sides and get log2(2^x)=log2(8) = 3. To solve x^2 = 16, you want to apply the inverse of f(x)=x^2 to both sides, but since f(x)=x^2 isn't invertible, you have to split it into two cases. If x is positive, g(x) = sqrt(x) is the inverse of f, but if x is negative, g(x) = -sqrt(x) is the inverse. So the solutions are x = +4 and -4.
Community AnswerFor one thing, any time you solve an equation. To solve x+4 = 7, you apply the inverse function of f(x) = x+4, that is g(x) = x-4, to both sides (x+4)-4 = 7-4 . To solve 2^x = 8, the inverse function of 2^x is log2(x), so you apply log base 2 to both sides and get log2(2^x)=log2(8) = 3. To solve x^2 = 16, you want to apply the inverse of f(x)=x^2 to both sides, but since f(x)=x^2 isn't invertible, you have to split it into two cases. If x is positive, g(x) = sqrt(x) is the inverse of f, but if x is negative, g(x) = -sqrt(x) is the inverse. So the solutions are x = +4 and -4. -
QuestionWhat inverse operations do I use to solve equations?
 DanoyachtcaptTop AnswererThe inverse of any number is that number divided into 1, as in 1/N.
DanoyachtcaptTop AnswererThe inverse of any number is that number divided into 1, as in 1/N.
References
- ↑ https://www.khanacademy.org/math/algebra2/manipulating-functions/introduction-to-inverses-of-functions/a/intro-to-inverse-functions
- ↑ https://www.purplemath.com/modules/invrsfcn3.htm
- ↑ https://tutorial.math.lamar.edu/classes/alg/inversefunctions.aspx
- ↑ https://www.ck12.org/trigonometry/inverse-trig-functions-using-algebra/lesson/inverse-of-functions-through-algebraic-manipulation-trig/
- ↑ https://www.khanacademy.org/math/algebra-home/alg-functions/alg-finding-inverse-functions/a/finding-inverse-functions
- ↑ https://www.mathsisfun.com/sets/function-inverse.html
- ↑ https://mathbitsnotebook.com/Algebra2/Functions/FNInverseFunctions.html