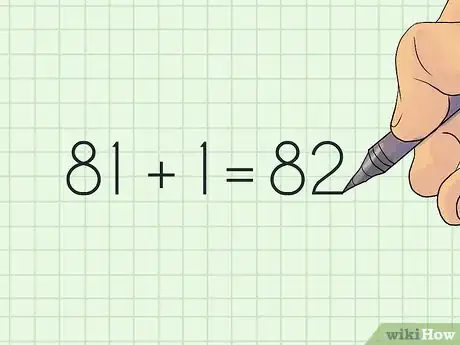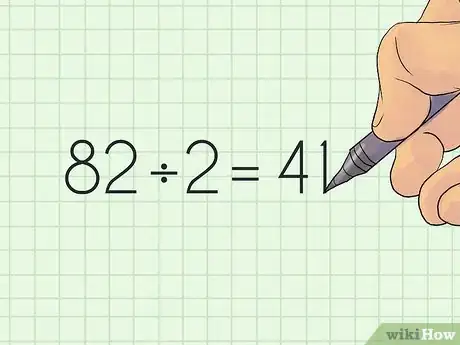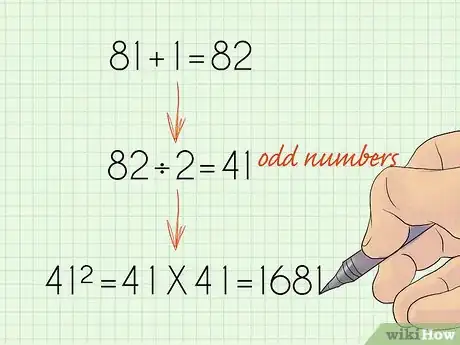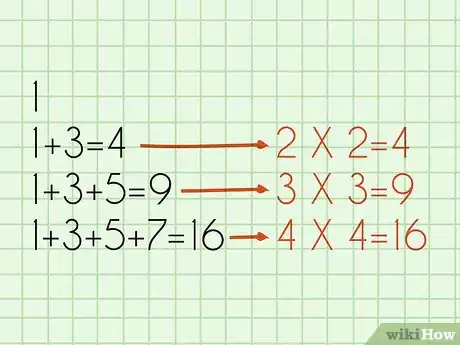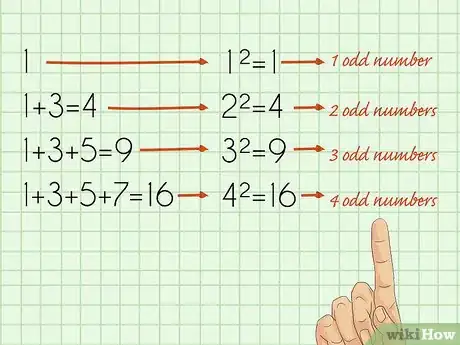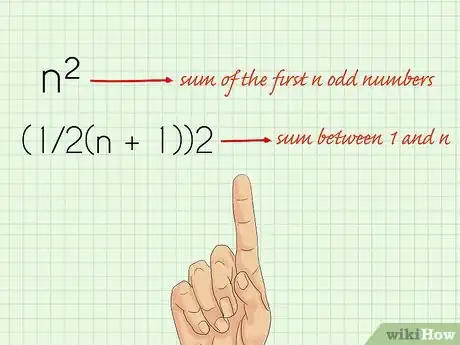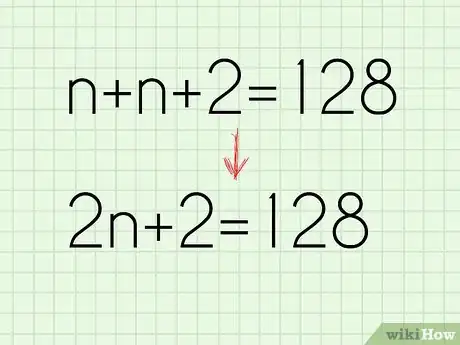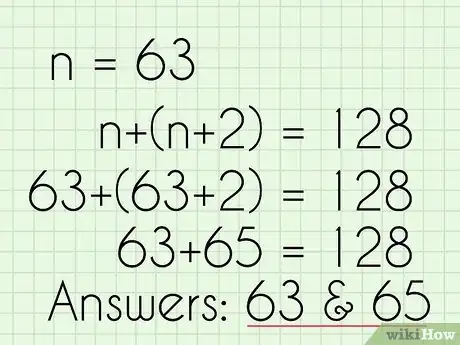How to Add a Sequence of Consecutive Odd Numbers

Co-authored by wikiHow Staff

Last Updated: March 7, 2023

You can add a series of consecutive odd numbers manually, but there is a much easier way to do it, especially if you are dealing with a lot of numbers. Once you master a simple formula, you will be able to add these numbers in no time without the use of a calculator. There is also a simple way to find out which consecutive numbers add up to a given sum.

Part 1

Part 1 of 3:

Applying the Formula for Adding a Sequence of Consecutive Odd Numbers

1
Choose an ending point. Before you get started, you need to determine what the last consecutive number in your set will be. This formula can help you add any number of consecutive odd numbers starting with 1.
- If you're working on an assignment, this number will be given to you. For example, if the question asks you to find the sum of all consecutive odd numbers from 1 through 81, your ending point is 81.
2
Add 1. The next step is to simply add 1 to your ending point. You should now have an even number, which is essential for the next step.^{[1]
X
Research source}
- For example, if your ending point is 81, 81 + 1 = 82.
Advertisement
3
Divide by 2. Once you have an even number, you should divide this by 2. This will give you an odd number that is equal to the number of digits that are being added together.^{[2]
X
Research source}
- For example, 82 / 2 = 41.
4
Square the quotient. The last step is to square that last number, or multiply it by itself. Once you do this, you will have your answer.
- For example, 41 x 41 = 1681. This means the sum of all consecutive odd numbers from 1 through 81 is 1681.

Part 2

Part 2 of 3:

Understanding Why the Formula Works

1
Observe the pattern. The key to understanding this formula is to recognize the underlying pattern. The sum of any set of consecutive odd numbers starting with 1 is always equal to the square of the number of digits that were added together.^{[3]
X
Research source}
- Sum of first odd number = 1
- Sum of first two odd numbers = 1 + 3 = 4 (= 2 x 2).
- Sum of first three odd numbers = 1 + 3 + 5 = 9 (= 3 x 3).
- Sum of first four odd numbers = 1 + 3 + 5 + 7 = 16 (= 4 x 4).
2
Understand the interim data. By solving this problem, you learned more than the sum of the numbers. You also learned how many consecutive digits were added together: 41! This is because the number of digits added together is always equal to the square root of the sum.
- Sum of first odd number = 1. The square root of 1 is 1, and only one digit was added.
- Sum of first two odd numbers = 1 + 3 = 4. The square root of 4 is 2, and two digits were added.
- Sum of first three odd numbers = 1 + 3 + 5 = 9. The square root of 9 is 3, and three digits were added.
- Sum of first four odd numbers = 1 + 3 + 5 + 7 = 16. The square root of 16 is 4, and four digits were added.
3
Generalize the formula. Once you understand the formula and how it works, you can write it down in a format that will be applicable no matter what numbers you are dealing with. The formula to find the sum of the first n odd numbers is n x n or n squared.
- For example, if you plugged 41 in for n, you would have 41 x 41, or 1681, which is equal to the sum of the first 41 odd numbers.
- If you don't know how many numbers you are dealing with, the formula to determine the sum between 1 and n is (1/2(n + 1))²

Part 3

Part 3 of 3:

Determining Which Consecutive Odd Numbers Add Up to a Sum

1
Understand the difference between the two types of problems. If you are given a series of consecutive odd numbers and are asked to find their sum, you should use the (1/2(n + 1))² equation. If, on the other hand, you have been given a sum and asked to find the series of consecutive odd numbers that adds up to that sum, you will need to use a different formula all together.
2
Let n equal the first number. To find out what consecutive odd numbers add up to a given sum, you will have to create an algebraic formula. Start by using n to represent the first number in the sequence.^{[4]
X
Research source}
3
Write the remaining numbers in terms of n. You will need to determine how to write the rest of the numbers in the sequence in terms of n. Because they are all consecutive odd numbers, there will be a difference of two between each number.
- This means the second number in the series will be n + 2, the third will be n + 4, etc.
4
Complete your formula. Once you know how to represent each number in the series, it is time to write out your formula. The left side of your formula should represent the numbers in the series, and the right side should represent their sum.
- For example, if you have been asked to find a series of two consecutive odd numbers that add up to 128, you would write n + n + 2 = 128.
5
Simplify the equation. If you have more than one n on the left side of your equation, add them together. This will make it much easier to solve.^{[5]
X
Research source}
- For example, n + n + 2 = 128 simplifies to 2n + 2 = 128.
6
Isolate n. The last step to solving this equation is to get n by itself on one side of the equation. Remember that whatever changes you make to one side of the equation, you must make to the other side as well.
- Deal with addition and subtraction first. In this case, you need to subtract 2 from both sides of the equation to get n by itself , so 2n = 126.
- Then deal with multiplication and division. In this case, you need to divide both sides by 2 in order to isolate n, so n = 63.
7
Write out your answer. At this point, you know that n = 63, but you are not quite done. You need to make sure that you completely answer the question that was asked. If the question asks you what series of consecutive, odd numbers adds up to a given sum, you must write out all of the numbers.
- The answer to this problem is 63 and 65 because n = 63 and n + 2 = 65.
- It's always a good idea to check your work by plugging your numbers back into the equation. If they don't equal the given sum, go back and try again.

Community Q&A

Question

Addition of two-digit consecutive numbers, divide by 2 and subtract by the number started with, why do I always get .5?

Donagan

Top Answerer

Whenever you add together two consecutive numbers, the sum is an odd number. When you divide any odd number by two, you get a quotient beginning with the first digit or digits you started with and ending in .5. Then if you subtract the first digit(s) from the quotient, you're left with .5. This is true when working with any consecutive numbers, two-digit or otherwise.
Question

What about when it doesn't start with 1?

Orangejews

Community Answer

To add say 21+23+...91, just pretend it started at 1 and subtract off the excess. First use the formula on 1 + ...91 then subtract the part you wanted to leave out 1+ ...+ 19 which you can sum with the same formula.
Question

In a sequence of 12 consecutive odd numbers, the sum of the first 5 numbers is 425. What is the sum of the last 5 numbers in the sequence?

Community Answer

The sum of the last 5 numbers in the sequence make up 495. If we state that "n" represents any odd number and start our sequence: n + (n+2) + (n+4) + (n+6) + (n+8) = 425, where n = 81. If we continued this sequence, the last 5 consecutive odd numbers can be represented by: (n+14) + (n+16) + (n+18) + (n+20) + (n+22). By substituting n = 81 into this sequence, we get 495. Another way is to write out 12 consecutive odd numbers starting with 81 and then adding the last 5 numbers.