Z-Scores and Location in a Distribution

A $z$-score is the signed number of standard deviations an observation is above the mean of a distribution. Thus, a positive $z$-score represents an observation above the mean, while a negative $z$-score represents an observation below the mean. We obtain a $z$-score through a conversion process known as standardizing or normalizing.

$z$-scores are also called standard scores, $z$-values, normal scores or standardized variables. The use of "$z$" is because the normal distribution is also known as the "$z$ distribution." $z$-scores are most frequently used to compare a sample to a standard normal deviate (standard normal distribution, with $\mu = 0$ and $\sigma =1$).

While $z$-scores can be defined without assumptions of normality, they can only be defined if one knows the population parameters. If one only has a sample set, then the analogous computation with sample mean and sample standard deviation yields the Student's $t$-statistic.

Calculation From a Raw Score

A raw score is an original datum, or observation, that has not been transformed. This may include, for example, the original result obtained by a student on a test (i.e., the number of correctly answered items) as opposed to that score after transformation to a standard score or percentile rank. The $z$-score, in turn, provides an assessment of how off-target a process is operating.

The conversion of a raw score, $x$, to a $z$-score can be performed using the following equation:

$z=\dfrac { x-\mu }{ \sigma }$

where $\mu$ is the mean of the population and $\sigma$ is the standard deviation of the population. The absolute value of $z$ represents the distance between the raw score and the population mean in units of the standard deviation. $z$ is negative when the raw score is below the mean and positive when the raw score is above the mean.

A key point is that calculating $z$ requires the population mean and the population standard deviation, not the sample mean nor sample deviation. It requires knowing the population parameters, not the statistics of a sample drawn from the population of interest. However, in cases where it is impossible to measure every member of a population, the standard deviation may be estimated using a random sample.

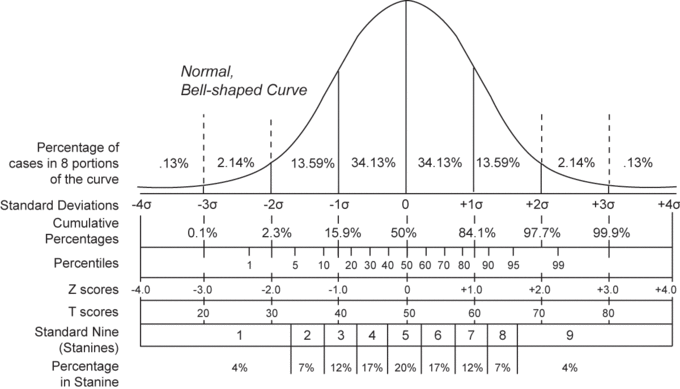
Normal Distribution and Scales

Shown here is a chart comparing the various grading methods in a normal distribution. $z$-scores for this standard normal distribution can be seen in between percentiles and $t$-scores.