An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis. It is most often used when comparing statistical models that have been fitted to a data set, in order to identify the model that best fits the population from which the data were sampled. Exact F-tests mainly arise when the models have been fitted to the data using least squares. The name was coined by George W. Snedecor, in honour of Sir Ronald A. Fisher. Fisher initially developed the statistic as the variance ratio in the 1920s.
The F-test is sensitive to non-normality. In the analysis of variance (ANOVA), alternative tests include Levene's test, Bartlett's test, and the Brown–Forsythe test. However, when any of these tests are conducted to test the underlying assumption of homoscedasticity (i.e., homogeneity of variance), as a preliminary step to testing for mean effects, there is an increase in the experiment-wise type I error rate.
Examples of F-tests include:
- The hypothesis that the means and standard deviations of several populations are equal. (Note that all populations involved must be assumed to be normally distributed.) This is perhaps the best-known F-test, and plays an important role in the analysis of variance (ANOVA).
- The hypothesis that a proposed regression model fits the data well (lack-of-fit sum of squares).
- The hypothesis that a data set in a regression analysis follows the simpler of two proposed linear models that are nested within each other.
- Scheffé's method for multiple comparisons adjustment in linear models.
The F-Distribution
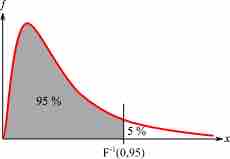
F-distribution
The F-distribution is skewed to the right and begins at the x-axis, meaning that F-values are always positive.
The F-distribution exhibits the following properties, as illustrated in the above graph:
- The curve is not symmetrical but is skewed to the right.
- There is a different curve for each set of degrees of freedom.
- The F-statistic is greater than or equal to zero.
- As the degrees of freedom for the numerator and for the denominator get larger, the curve approximates the normal.
The F-statistic also has a common table of values, as do z-scores and t-scores.