One of the major applications of statistics is estimating population parameters from sample statistics. For example, a poll may seek to estimate the proportion of adult residents of a city that support a proposition to build a new sports stadium. Out of a random sample of 200 people, 106 say they support the proposition. Thus in the sample, 0.53 (
It is rare that the actual population parameter would equal the sample statistic. In our example, it is unlikely that, if we polled the entire adult population of the city, exactly 53% of the population would be in favor of the proposition. Instead, we use confidence intervals to provide a range of likely values for the parameter.
For this reason, point estimates are usually supplemented by interval estimates or confidence intervals. Confidence intervals are intervals constructed using a method that contains the population parameter a specified proportion of the time. For example, if the pollster used a method that contains the parameter 95% of the time it is used, he or she would arrive at the following 95% confidence interval:
Error and Bias
Assume that
All measurements have some error associated with them. Random errors occur in all data sets and are sometimes known as non-systematic errors. Random errors can arise from estimation of data values, imprecision of instruments, etc. For example, if you are reading lengths off a ruler, random errors will arise in each measurement as a result of estimating between which two lines the length lies. Bias is sometimes known as systematic error. Bias in a data set occurs when a value is consistently under or overestimated. Bias can also arise from forgetting to take into account a correction factor or from instruments that are not properly calibrated. Bias leads to a sample mean that is either lower or higher than the true mean .
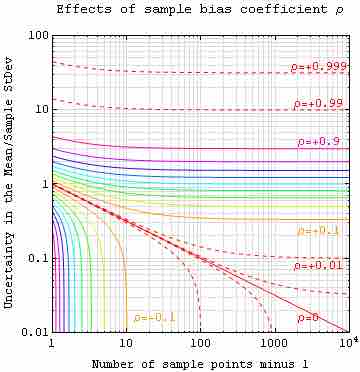
Sample Bias Coefficient
An estimate of expected error in the sample mean of variable
Mean-Squared Error
The mean squared error (MSE) of