Determining Sample Size Required to Estimate the Population Mean ($\mu$ )
Before calculating a point estimate and creating a confidence interval, a sample must be taken. Often, the number of data values needed in a sample to obtain a particular level of confidence within a given error needs to be determined before taking the sample. If the sample is too small, the result may not be useful, and if the sample is too big, both time and money are wasted in the sampling. The following text discusses how to determine the minimum sample size needed to make an estimate given the desired confidence level and the observed standard deviation.
First, consider the margin of error,
To change the size of the error (
As the confidence increases, the margin of error (
As the sample size (
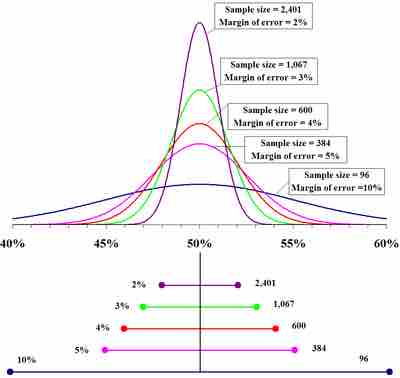
Sample size compared to margin of error
The top portion of this graphic depicts probability densities that show the relative likelihood that the "true" percentage is in a particular area given a reported percentage of 50%. The bottom portion shows the 95% confidence intervals (horizontal line segments), the corresponding margins of error (on the left), and sample sizes (on the right). In other words, for each sample size, one is 95% confident that the "true" percentage is in the region indicated by the corresponding segment. The larger the sample is, the smaller the margin of error is.
where
Since the population standard deviation is often unknown, the sample standard deviation from a previous sample of size
Example
Suppose the scores on a statistics final are normally distributed with a standard deviation of 10 points. Construct a 95% confidence interval with an error of no more than 2 points.
Solution
So, a sample of size of 68 must be taken to create a 95% confidence interval with an error of no more than 2 points.
Determining Sample Size Required to Estimate Population Proportion ($p$ )
The calculations for determining sample size to estimate a proportion (
where:
-
$p' = \frac{x}{n}$ is the point estimate for the population proportion -
$x$ is the number of successes in the sample -
$n$ is the number in the sample; and -
$q' = 1-p'$
Then, solving for the minimum sample size
Example
The Mesa College mathematics department has noticed that a number of students place in a non-transfer level course and only need a 6 week refresher rather than an entire semester long course. If it is thought that about 10% of the students fall in this category, how many must the department survey if they wish to be 95% certain that the true population proportion is within
Solution
So, a sample of size of 139 must be taken to create a 95% confidence interval with an error of