Interval estimation is the use of sample data to calculate an interval of possible (or probable) values of an unknown population parameter. The most prevalent forms of interval estimation are:
- confidence intervals (a frequentist method); and
- credible intervals (a Bayesian method).
Other common approaches to interval estimation are:
- Tolerance intervals
- Prediction intervals - used mainly in Regression Analysis
- Likelihood intervals
Example: Estimating the Population Mean
How can we construct a confidence interval for an unknown population mean
- The data is from a simple random sample of size
$n$ from the population of interest. - Data from the population have a Normal distribution with mean and standard deviation. These are both unknown parameters.
- The method for calculating a confidence interval assumes that individual observations are independent.
The sample mean
The $t$ -Distribution
When we do not know
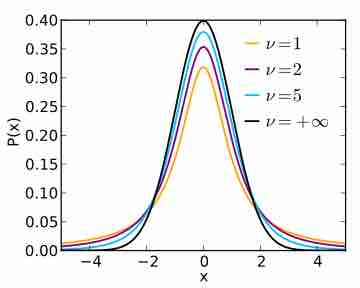
$t$ -Distribution
A plot of the
If we wanted to estimate the population mean, we can now put together everything we've learned. First, draw a simple random sample from a population with an unknown mean. A confidence interval for is calculated by:
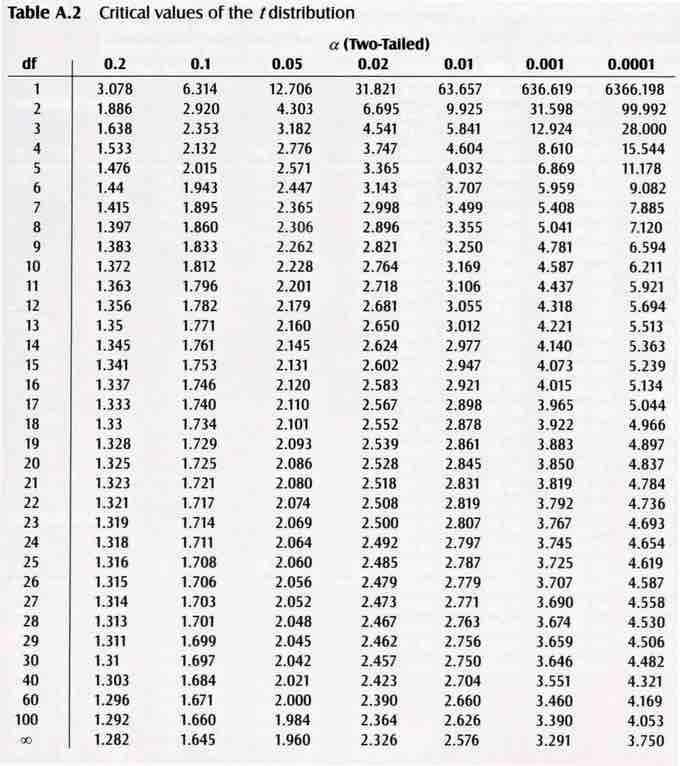
$t$ -Table
Critical values of the