Step By Step Example of a Confidence Interval for a Mean—Standard Deviation Unknown
Suppose you do a study of acupuncture to determine how effective it is in relieving pain. You measure sensory rates for 15 random subjects with the results given below:
8.6, 9.4, 7.9, 6.8, 8.3, 7.3, 9.2, 9.6, 8.7, 11.4, 10.3, 5.4, 8.1, 5.5, 6.9.
Use the sample data to construct a 95% confidence interval for the mean sensory rate for the populations (assumed normal) from which you took this data.
We have the following guidelines for such a problem:
- Plan: State what we need to know.
- Model: Think about the assumptions and check the conditions.
- State the parameters and the sampling model.
- Mechanics:
$\text{CL} = 0.95$ , so$\alpha = 1-\text{CL} = 1-0.95 = 0.05$ . The area to the right of$t_{0.25}$ is$1-0.025 = 0.975$ ; so$t_{0.025, 14} = 2.14$ . - Conclusion: Interpret your result in the proper context, and relate it to the original question.
1. In our example, we are asked to find a 95% confidence interval for the mean sensory rate,
2. We have the following conditions:
- Randomization Condition: The sample is a random sample.
- Independence Assumption: It is reasonable to think that the sensory rates of 15 subjects are independent.
- 10% Condition: We assume the acupuncture population is over 150, so 15 subjects is less than 10% of the population.
- Sample Size Condition: Since the distribution of mean sensory rates is normal, our sample of 15 is large enough.
- Nearly Normal Condition: We should do a box plot and histogram to check this. Even though the data is slightly skewed, it is unimodal (and there are no outliers) so we can use the model.
3. The conditions are satisfied and
4.
The 95% confidence interval for the mean score is
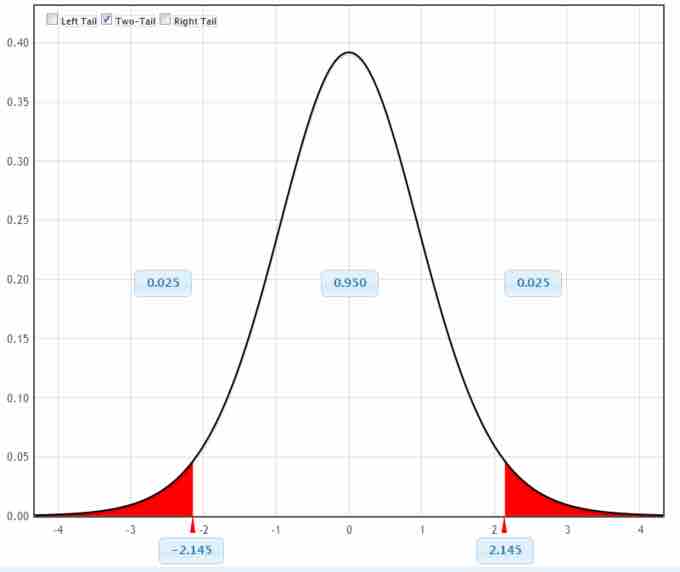
Graphical Representation
This figure is a graphical representation of the confidence interval we calculated in this example.
5. We are 95% confident that the interval from 7.30 to 9.15 contains the true mean score of all the sensory rates. 95% of all confidence intervals constructed in this way contain the true mean sensory rate score.
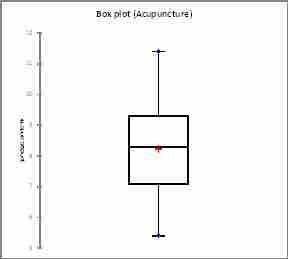
Box Plot
This figure is a box plot for the data set in our example.
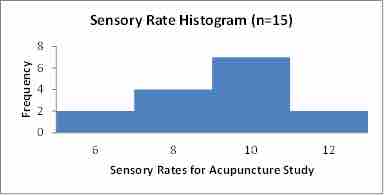
Histogram
This figure is a histogram for the data set in our example.