Sample Average vs. Population Average
The sample average (also called the sample mean) is often referred to as the arithmetic mean of a sample, or simply,
For a finite population, the population mean of a property is equal to the arithmetic mean of the given property while considering every member of the population. For example, the population mean height is equal to the sum of the heights of every individual divided by the total number of individuals.The sample mean may differ from the population mean, especially for small samples. The law of large numbers dictates that the larger the size of the sample, the more likely it is that the sample mean will be close to the population mean.
Calculation of the Sample Mean
The arithmetic mean is the "standard" average, often simply called the "mean". It can be calculated taking the sum of every piece of data and dividing that sum by the total number of data points:
For example, the arithmetic mean of five values: 4, 36, 45, 50, 75 is:
The mean may often be confused with the median, mode or range. The mean is the arithmetic average of a set of values, or distribution; however, for skewed distributions, the mean is not necessarily the same as the middle value (median), or the most likely (mode). For example, mean income is skewed upwards by a small number of people with very large incomes, so that the majority have an income lower than the mean. By contrast, the median income is the level at which half the population is below and half is above. The mode income is the most likely income, and favors the larger number of people with lower incomes. The median or mode are often more intuitive measures of such data .
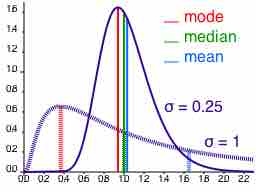
Measures of Central Tendency
This graph shows where the mean, median, and mode fall in two different distributions (one is slightly skewed left and one is highly skewed right).