Researchers often want to know how two or more variables are related. For example, is there a relationship between the grade on the second math exam a student takes and the grade on the final exam? If there is a relationship, what is it and how strong is it? As another example, your income may be determined by your education and your profession. The amount you pay a repair person for labor is often determined by an initial amount plus an hourly fee. These are all examples of a statistical factor known as correlation. Note that the type of data described in these examples is bivariate ("bi" for two variables). In reality, statisticians use multivariate data, meaning many variables. As in our previous example, your income may be determined by your education, profession, years of experience or ability.
Correlation and Dependence
Dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence. Familiar examples of dependent phenomena include the correlation between the physical statures of parents and their offspring and the correlation between the demand for a product and its price. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice.
For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling; however, statistical dependence is not sufficient to demonstrate the presence of such a causal relationship (i.e., correlation does not imply causation).
Formally, dependence refers to any situation in which random variables do not satisfy a mathematical condition of probabilistic independence. In loose usage, correlation can refer to any departure of two or more random variables from independence, but technically it refers to any of several more specialized types of relationship between mean values.
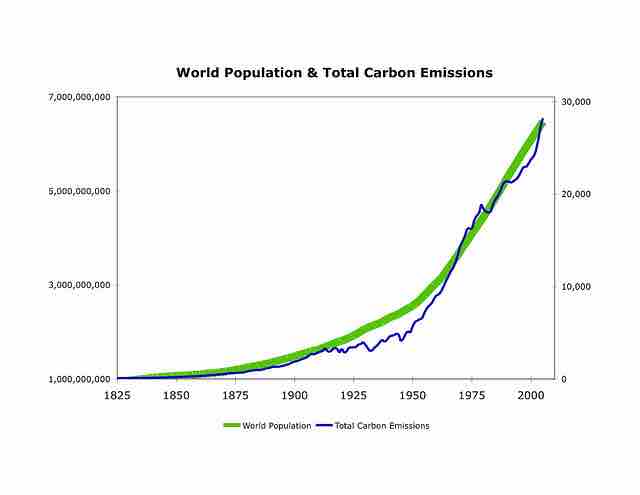
Correlation
This graph shows a positive correlation between world population and total carbon emissions.