A scatter plot, or diagram, is a type of mathematical diagram using Cartesian coordinates to display values for two variables in a set of data. The data is displayed as a collection of points, each having the value of one variable determining the position on the horizontal axis, and the value of the other variable determining the position on the vertical axis.
In the case of an experiment, a scatter plot is used when a variable exists that is below the control of the experimenter. The controlled parameter (or independent variable) is customarily plotted along the horizontal axis, while the measured (or dependent variable) is customarily plotted along the vertical axis. If no dependent variable exists, either type of variable can be plotted on either axis, and a scatter plot will illustrate only the degree of correlation (not causation) between two variables. This is the context in which we view scatter diagrams.
Relevance to Correlation
A scatter plot shows the direction and strength of a relationship between the variables. A clear direction happens given one of the following:
- High values of one variable occurring with high values of the other variable or low values of one variable occurring with low values of the other variable.
- High values of one variable occurring with low values of the other variable.
You can determine the strength of the relationship by looking at the scatter plot and seeing how close the points are to a line, a power function, an exponential function, or to some other type of function. When you look at a scatterplot, you want to notice the overall pattern and any deviations from the pattern. The following scatterplot examples illustrate these concepts .
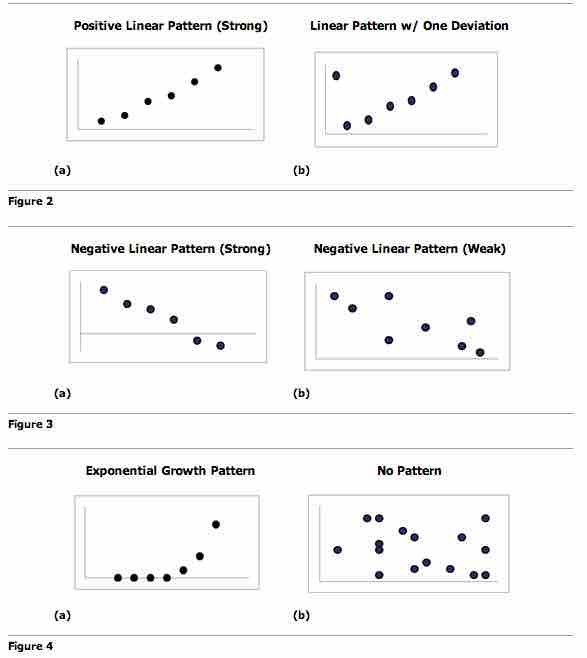
Scatter Plot Patterns
An illustration of the various patterns that scatter plots can visualize.
Trend Lines
To study the correlation between the variables, one can draw a line of best fit (known as a "trend line"). An equation for the correlation between the variables can be determined by established best-fit procedures. For a linear correlation, the best-fit procedure is known as linear regression and is guaranteed to generate a correct solution in a finite time. No universal best-fit procedure is guaranteed to generate a correct solution for arbitrary relationships.
Other Uses of Scatter Plots
A scatter plot is also useful to show how two comparable data sets agree with each other. In this case, an identity line (i.e., a
One of the most powerful aspects of a scatter plot, however, is its ability to show nonlinear relationships between variables. Furthermore, if the data is represented by a mixed model of simple relationships, these relationships will be visually evident as superimposed patterns.