In mechanics (physics), Hooke's law is an approximation of the response of elastic (i.e., springlike) bodies. It states: the extension of a spring is in direct proportion with the load applied to it . For instance, the spring is pulled downwards with either no load, Fp, or twice Fp.
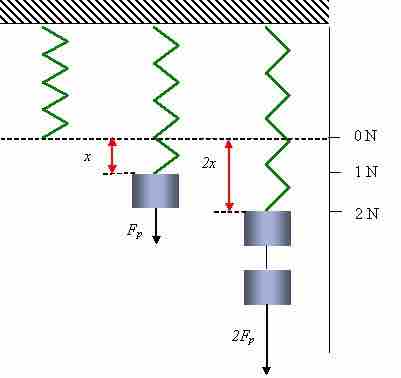
Diagram of Hooke's Law
The extension of the spring is linearly proportional to the force.
Many materials obey this law of elasticity as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law is a useful approximation are known as linear-elastic or "Hookean" materials. Hookean materials are broadly defined and include springs as well as muscular layers of the heart. In simple terms, Hooke's law says that stress is directly proportional to strain. Mathematically, Hooke's law is stated as:
where:
- x is the displacement of the spring's end from its equilibrium position (a distance, in SI units: meters);
- F is the restoring force exerted by the spring on that end (in SI units: N or kg·m/s2); and
- k is a constant called the rate or spring constant (in SI units: N/m or kg/s2). When this holds, the behavior is said to be linear. If shown on a graph, the line should show a direct variation.
It's possible for multiple springs to act on the same point. In such a case, Hooke's law can still be applied. As with any other set of forces, the forces of many springs can be combined into one resultant force.
When Hooke's law holds, the behavior is linear; if shown on a graph, the line depicting force as a function of displacement should show a direct variation. There is a negative sign on the right hand side of the equation because the restoring force always acts in the opposite direction of the displacement (for example, when a spring is stretched to the left, it pulls back to the right).
Hooke's law is named after the 17th century British physicist Robert Hooke, and was first stated in 1660 as a Latin anagram, whose solution Hooke published in 1678 as Ut tensio, sic vis, meaning, "As the extension, so the force."
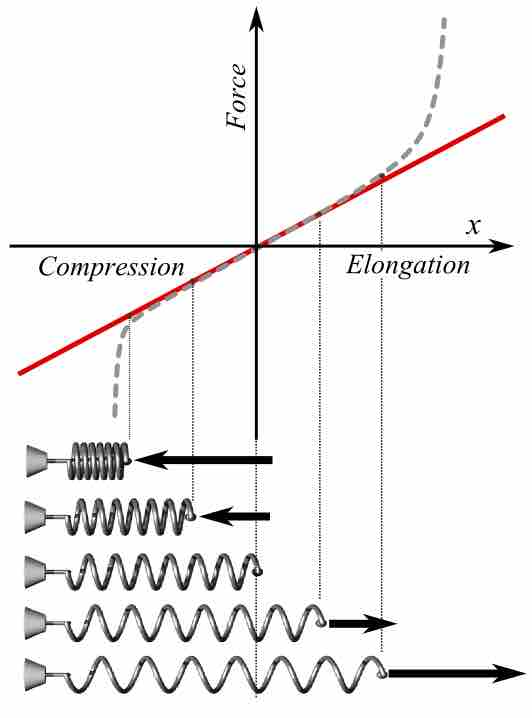
Hooke's Law
The red line in this graph illustrates how force, F, varies with position according to Hooke's law. The slope of this line corresponds to the spring constant k. The dotted line shows what the actual (experimental) plot of force might look like. The pictures of spring states at the bottom of the graph correspond to some points of the plot; the middle one is in the relaxed state (no force applied).