Elastic Potential Energy
In order to produce a deformation, work must be done. That is, a force must be exerted through a distance, whether you pluck a guitar string or compress a car spring. If the only result is deformation and no work goes into thermal, sound, or kinetic energy, then all the work is initially stored in the deformed object as some form of potential energy. Elastic energy is the potential mechanical energy stored in the configuration of a material or physical system when work is performed to distort its volume or shape. For example, the potential energy PEel stored in a spring is
where k is the elastic constant and x is the displacement.
It is possible to calculate the work done in deforming a system in order to find the energy stored. This work is performed by an applied force Fapp. The applied force is exactly opposite to the restoring force (action-reaction), and so
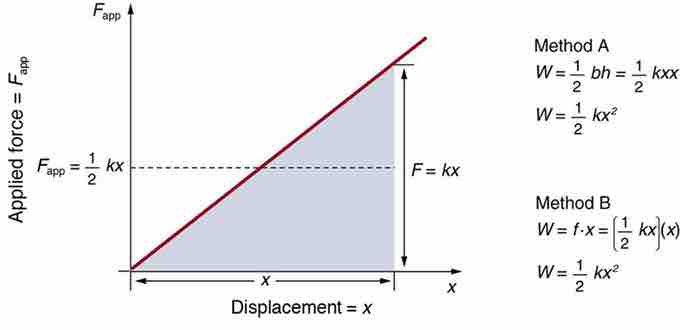
Applied force versus deformation
A graph of applied force versus distance for the deformation of a system that can be described by Hooke's law is displayed. The work done on the system equals the area under the graph or the area of the triangle, which is half its base multiplied by its height, or
Elastic energy of or within a substance is static energy of configuration. It corresponds to energy stored principally by changing the inter-atomic distances between nuclei. Thermal energy is the randomized distribution of kinetic energy within the material, resulting in statistical fluctuations of the material about the equilibrium configuration. There is some interaction, however. For example, for some solid objects, twisting, bending, and other distortions may generate thermal energy, causing the material's temperature to rise. This energy can also produce macroscopic vibrations sufficiently lacking in randomization to lead to oscillations that are merely the exchange between (elastic) potential energy within the object and the kinetic energy of motion of the object as a whole.