Period and Frequency
The usual physics terminology for motion that repeats itself over and over is periodic motion, and the time required for one repetition is called the period, often expressed as the letter T. (The symbol P is not used because of the possible confusion with momentum. ) One complete repetition of the motion is called a cycle. The frequency is defined as the number of cycles per unit time. Frequency is usually denoted by a Latin letter f or by a Greek letter ν (nu). Note that period and frequency are reciprocals of each other .
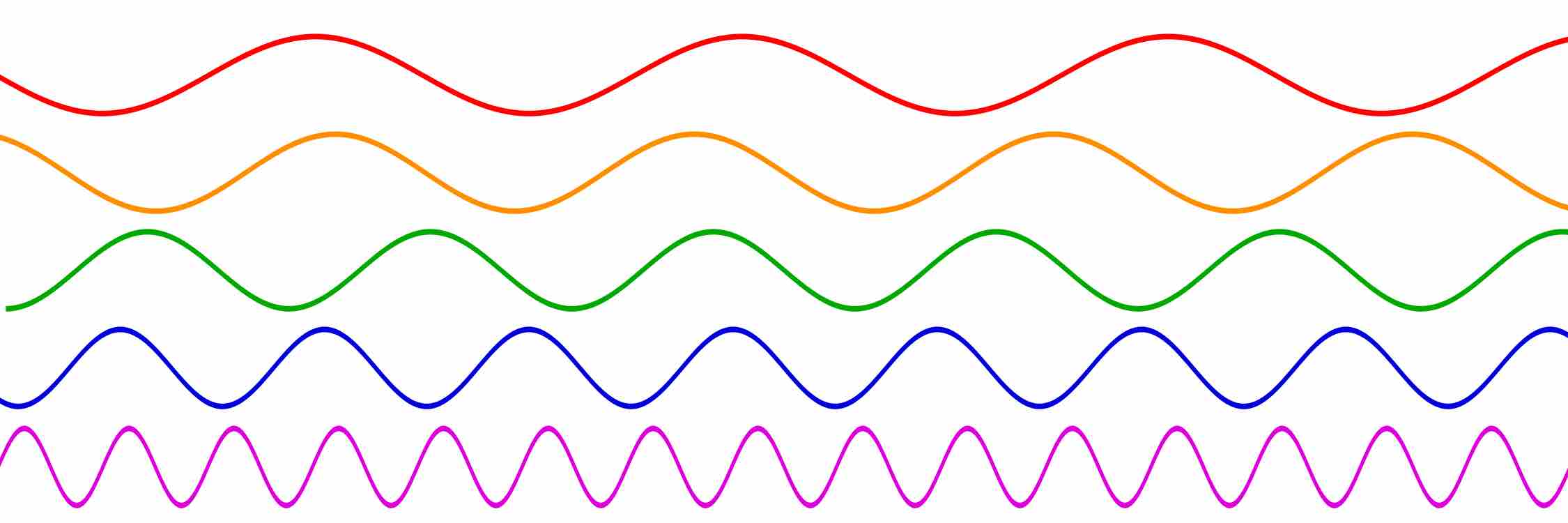
Sinusoidal Waves of Varying Frequencies
Sinusoidal waves of various frequencies; the bottom waves have higher frequencies than those above. The horizontal axis represents time.
For example, if a newborn baby's heart beats at a frequency of 120 times a minute, its period (the interval between beats) is half a second. If you calibrate your intuition so that you expect large frequencies to be paired with short periods, and vice versa, you may avoid some embarrassing mistakes on physics exams.
Units
In SI units, the unit of frequency is the hertz (Hz), named after the German physicist Heinrich Hertz: 1 Hz indicates that an event repeats once per second. A traditional unit of measure used with rotating mechanical devices is revolutions per minute, abbreviated RPM. 60 RPM equals one hertz (i.e., one revolution per second, or a period of one second). The SI unit for period is the second.
Angular Frequency
Often periodic motion is best expressed in terms of angular frequency, represented by the Greek letter ω (omega). Angular frequency refers to the angular displacement per unit time (e.g., in rotation) or the rate of change of the phase of a sinusoidal waveform (e.g., in oscillations and waves), or as the rate of change of the argument of the sine function.

Locomotive Wheels
The locomotive's wheels spin at a frequency of f cycles per second, which can also be described as ω radians per second. The mechanical linkages allow the linear vibration of the steam engine's pistons, at frequency f, to drive the wheels.
Angular frequency is often represented in units of radians per second (recall there are 2π radians in a circle).