Unit Vectors and Multiplication by a Scalar

In addition to adding vectors, vectors can also be multiplied by constants known as scalars. Scalars are distinct from vectors in that they are represented by a magnitude but no direction. Examples of scalars include an object's mass, height, or volume.

When multiplying a vector by a scalar, the direction of the vector is unchanged and the magnitude is multiplied by the magnitude of the scalar . This results in a new vector arrow pointing in the same direction as the old one but with a longer or shorter length. You can also accomplish scalar multiplication through the use of a vector's components. Once you have the vector's components, multiply each of the components by the scalar to get the new components and thus the new vector.

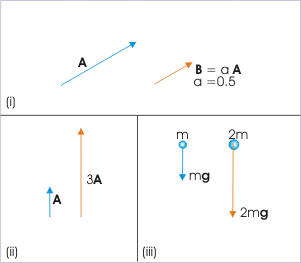
Scalar Multiplication

(i) Multiplying the vector A by 0.5 halves its length. (ii) Multiplying the vector A by 3 triples its length. (iii) Increasing the mass (scalar) increases the force (vector).

A useful concept in the study of vectors and geometry is the concept of a unit vector. A unit vector is a vector with a length or magnitude of one. The unit vectors are different for different coordinates. In Cartesian coordinates the directions are x and y usually denoted $\hat{x}$ and $\hat{y}$. With the triangle above the letters referred to as a "hat". The unit vectors in Cartesian coordinates describe a circle known as the "unit circle" which has radius one. This can be seen by taking all the possible vectors of length one at all the possible angles in this coordinate system and placing them on the coordinates. If you were to draw a line around connecting all the heads of all the vectors together, you would get a circle of radius one.