Projectile motion is the motion of an object thrown, or projected, into the air, subject only to the force of gravity. The object is called a projectile, and its path is called its trajectory. The motion of falling objects is a simple one-dimensional type of projectile motion in which there is no horizontal movement. In two-dimensional projectile motion, such as that of a football or other thrown object, there is both a vertical and a horizontal component to the motion.
Projectile Motion
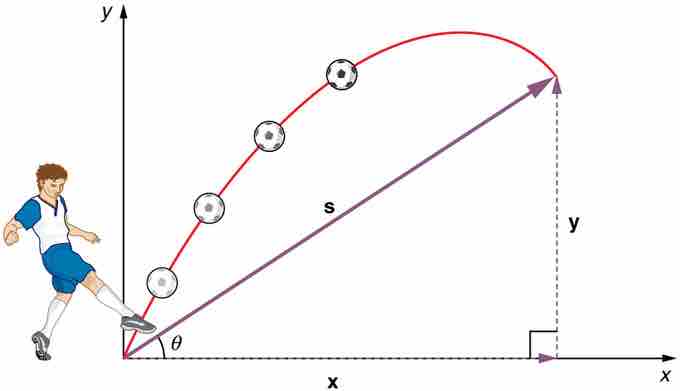
Throwing a rock or kicking a ball generally produces a projectile pattern of motion that has both a vertical and a horizontal component.
The most important fact to remember is that motion along perpendicular axes are independent and thus can be analyzed separately. The key to analyzing two-dimensional projectile motion is to break it into two motions, one along the horizontal axis and the other along the vertical. To describe motion we must deal with velocity and acceleration, as well as with displacement.
We will assume all forces except for gravity (such as air resistance and friction, for example) are negligible. The components of acceleration are then very simple:
We analyze two-dimensional projectile motion by breaking it into two independent one-dimensional motions along the vertical and horizontal axes. The horizontal motion is simple, because