Overview
Vectors are geometric representations of magnitude and direction which are often represented by straight arrows, starting at one point on a coordinate axis and ending at a different point. All vectors have a length, called the magnitude, which represents some quality of interest so that the vector may be compared to another vector. Vectors, being arrows, also have a direction. This differentiates them from scalars, which are mere numbers without a direction.
A vector is defined by its magnitude and its orientation with respect to a set of coordinates. It is often useful in analyzing vectors to break them into their component parts. For two-dimensional vectors, these components are horizontal and vertical. For three dimensional vectors, the magnitude component is the same, but the direction component is expressed in terms of
Decomposing a Vector
To visualize the process of decomposing a vector into its components, begin by drawing the vector from the origin of a set of coordinates. Next, draw a straight line from the origin along the x-axis until the line is even with the tip of the original vector. This is the horizontal component of the vector. To find the vertical component, draw a line straight up from the end of the horizontal vector until you reach the tip of the original vector. You should find you have a right triangle such that the original vector is the hypotenuse.
Decomposing a vector into horizontal and vertical components is a very useful technique in understanding physics problems. Whenever you see motion at an angle, you should think of it as moving horizontally and vertically at the same time. Simplifying vectors in this way can speed calculations and help to keep track of the motion of objects.
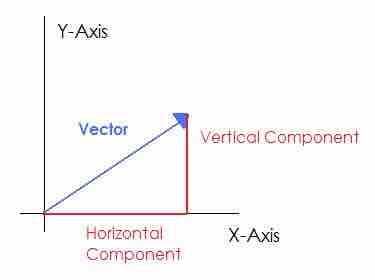
Components of a Vector
The original vector, defined relative to a set of axes. The horizontal component stretches from the start of the vector to its furthest x-coordinate. The vertical component stretches from the x-axis to the most vertical point on the vector. Together, the two components and the vector form a right triangle.