Constant Velocity

Motion with constant velocity is one of the simplest forms of motion. This type of motion occurs when an an object is moving (or sliding) in the presence of little or negligible friction, similar to that of a hockey puck sliding across the ice. To have a constant velocity, an object must have a constant speed in a constant direction. Constant direction constrains the object to motion to a straight path.

Newton's second law ($F=ma$) suggests that when a force is applied to an object, the object would experience acceleration. If the acceleration is 0, the object shouldn't have any external forces applied on it. Mathematically, this can be shown as the following:

$a = \frac{dv}{dt} = 0~\Rightarrow~ v = const$.

If an object is moving at constant velocity, the graph of distance vs. time ($x$ vs. $t$) shows the same change in position over each interval of time. Therefore the motion of an object at constant velocity is represented by a straight line: $x=x_0+vt$, where $x_0$ is the displacement when $t=0$ (or at the y-axis intercept).

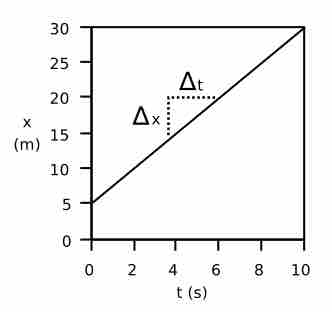
Motion with Constant Velocity

When an object is moving with constant velocity, it does not change direction nor speed and therefore is represented as a straight line when graphed as distance over time.

You can also obtain an object's velocity if you know its trace over time. Given a graph as in , we can calculate the velocity from the change in distance over the change in time. In graphical terms, the velocity can be interpreted as the slope of the line. The velocity can be positive or negative, and is indicated by the sign of our slope. This tells us in which direction the object moves.