Area Expansion

We learned about the linear expansion (in one dimension) in the previous Atom. Objects expand in all dimensions, and we can extend the thermal expansion for 1D to two (or three) dimensions. That is, their areas and volumes, as well as their lengths, increase with temperature.

Quiz

Before we look into details, here is an interesting question. Imagine that we have a rectangular sheet of metal with a circular hole in the middle. If the metal is heated, we can guess that the the piece, in general, will get larger due to thermal expansion. Now, what is going to happen with the circular hole in the middle? Is the hole going to be larger or smaller? Answer: Imagine that we have a similar metal sheet but without a hole. Draw an imaginary circular line representing the circular hole in our quiz. How does this imaginary circle change as the metal is heated? Yes. It will get bigger. Therefore, you can guess that the hole in our quiz will get larger.

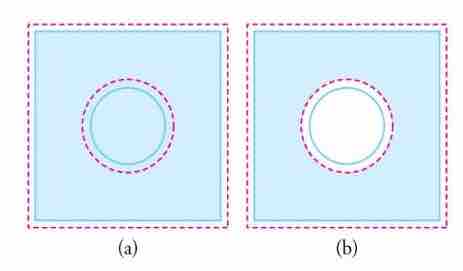
Fig 1

In general, objects expand in all directions as temperature increases. In these drawings, the original boundaries of the objects are shown with solid lines, and the expanded boundaries with dashed lines. (a) Area increases because both length and width increase. The area of a circular plug also increases. (b) If the plug is removed, the hole it leaves becomes larger with increasing temperature, just as if the expanding plug were still in place.

Area thermal expansion coefficient

The area thermal expansion coefficient relates the change in a material's area dimensions to a change in temperature. It is the fractional change in area per degree of temperature change. Ignoring pressure, we may write: $\alpha_A = \frac{1}{A} \frac{dA}{dT}$, where is some area of interest on the object, and dA/dT is the rate of change of that area per unit change in temperature. The change in the linear dimension can be estimated as: $\frac{\Delta A}{A} = \alpha_A \Delta T$. This equation works well as long as the linear expansion coefficient does not change much over the change in temperature $\Delta T$. If it does, the equation must be integrated.

Relationship to linear thermal expansion coefficient

For isotropic materials, and for small expansions, the linear thermal expansion coefficient is one half of the area coefficient. To derive the relationship, let's take a square of steel that has sides of length L. The original area will be A = L²,and the new area, after a temperature increase, will be $\begin{aligned} A + \Delta A &= (L + \Delta L)^2 \\ &= L^2 + 2L\Delta L + (\Delta L )^2 \\ &\approx L^2 + 2L\Delta L \\ &= A + 2 A \frac {\Delta L}{L} \end{aligned}$

The approximation holds for a sufficiently small $\Delta L$ campared to L. Since $\frac{\Delta A}{A} = 2 \frac{\Delta L}{L}$ from the equation above (and from the definitions of the thermal coefficients), we get $\alpha_A = 2 \alpha_L$.