Constant Pressure

Under a certain constraint (e.g., pressure), gases can expand or contract; depending on the type of constraint, the final state of the gas may change. For example, an ideal gas that expands while its temperature is kept constant (called isothermal process) will exist in a different state than a gas that expands while pressure stays constant (called isobaric process). This Atom addresses isobaric process and correlated terms. We will discuss isothermal process in a subsequent Atom.

Isobaric Process

An isobaric process is a thermodynamic process in which pressure stays constant: ΔP = 0. For an ideal gas, this means the volume of a gas is proportional to its temperature (historically, this is called Charles' law). Let's consider a case in which a gas does work on a piston at constant pressure P, referring to Fig 1 as illustration. Since the pressure is constant, the force exerted is constant and the work done is given as W=Fd, where F (=PA) is the force on the piston applied by the pressure and d is the displacement of the piston. Therefore, the work done by the gas (W) is:

$W = PAd$.

Because the change in volume of a cylinder is its cross-sectional area A times the displacement d, we see that Ad=ΔV, the change in volume. Thus,

$W= P \Delta V$

(as seen in Fig 2—isobaric process ). Note: if ΔV is positive, then W is positive, meaning that work is done by the gas on the outside world. Using the ideal gas law PV=NkT (P=const),

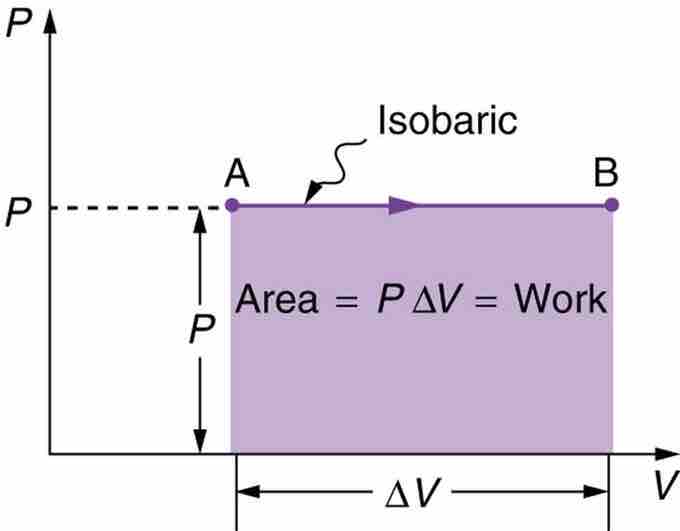
Fig 2

A graph of pressure versus volume for a constant-pressure, or isobaric process. The area under the curve equals the work done by the gas, since W=PΔV.

$W = Nk\Delta T$

(Eq. 1) for an ideal gas undergoing an isobaric process.

Monatomic Gas

According to the first law of thermodynamics,

$Q = \Delta U + W\,$

(Eq. 2), where W is work done by the system, U is internal energy, and Q is heat. The law says that the heat transferred to the system does work but also changes the internal energy of the system. Since,

$U = \frac{3}{2}NkT$ for a monatomic gas, we get $\Delta U = \frac{3}{2} Nk \Delta T$

(Eq. 3; for the details on internal energy, see our Atom on "Internal Energy of an Ideal Gas"). By using the Equations 1 and 3, Eq. 2 can be written as:

$Q = \frac{5}{2} N k \Delta T$ for monatomic gas in an isobaric process.

Specific Heat

Specific heat at constant pressure is defined by the following equation:

$Q = n c_P \Delta T$.

Here n is the amount of particles in a gas represented in moles. By noting that N=N_An and R = kN_A (N_A: Avogadro's number, R: universal gas constant), we derive:

$c_P = \frac{5}{2} kN_A = \frac{5}{2} R$ for a monatomic gas.