Parallel wires carrying current produce significant magnetic fields, which in turn produce significant forces on currents. The force felt between the wires is used to define the the standard unit of current, know as an amphere.
In , the field (B1) that I1 creates can be calculated as a function of current and wire separation (r):
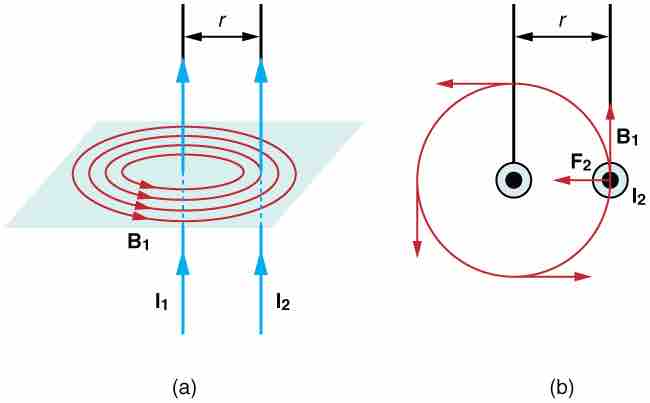
Magnetic fields and force exerted by parallel current-carrying wires.
Currents I1 and I2 flow in the same direction, separated by a distance of r.
The field B1 exerts a force on the wire containing I2. In the figure, this force is denoted as F2.
The force F2 exerts on wire 2 can be calculated as:
Given that the field is uniform along and perpendicular to wire 2, sin θ = sin 90 derees = 1. Thus the force simplifies to: F2=I2lB1
According to Newton's Third Law (F1=-F2), the forces on the two wires will be equal in magnitude and opposite in direction, so to simply we can use F instead of F2. Given that wires are often very long, it's often convenient to solve for force per unit length. Rearranging the previous equation and using the definition of B1 gives:
If the currents are in the same direction, the force attracts the wires. If the currents are in opposite directions, the force repels the wires.
The force between current-carrying wires is used as part of the operational definition of the ampere. For parallel wires placed one meter away from one another, each carrying one ampere, the force per meter is:
The final units come from replacing T with 1N/(A×m).
Incidentally, this value is the basis of the operational definition of the ampere. This means that one ampere of current through two infinitely long parallel conductors (separated by one meter in empty space and free of any other magnetic fields) causes a force of 2×10-7 N/m on each conductor.