Current running through a wire will produce both an electric field and a magnetic field. For a closed curve of length C, magnetic field (B) is related to current (IC) as in Ampere's Law, stated mathematically as:
In this equation, dl represents the differential of length of wire in the curved wire, and μ0 is the permeability of free space. This can be related to the Biot-Savart law. For a short, straight length of conductor (typically a wire) this law generally calculates partial magnetic field (dB) as a function of current for an infinitesimally small segment of wire (dl) at a point r distance away from the conductor:
In this equation, the r vector can be written as r̂ (the unit vector in direction of r), if the r3 term in the denominator is reduced to r2 (this is simply reducing like terms in a fraction). Integrating the previous differential equation, we find:
This relationship holds for constant current in a straight wire, in which magnetic field at a point due to all current elements comprising the straight wire is the same. As illustrated in the direction of the magnetic field can be determined using the right hand rule—pointing one's thumb in the direction of current, the curl of one's fingers indicates the direction of the magnetic field around the straight wire.
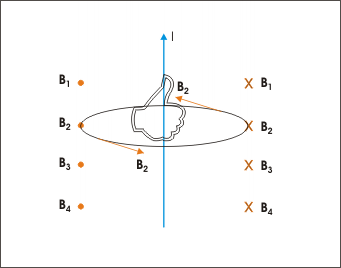
Direction of magnetic field
The direction of the magnetic field can be determined by the right hand rule.