Resistors in AC Circuits

In a circuit with a resistor and an AC power source, Ohm's law still applies (V = IR).

Learning Objective

Apply Ohm's law to determine current and voltage in an AC circuit

Key Points

With an AC voltage given by: $V = V_0 sin(2\pi \nu t)$ the current in the circuit is given as: $I = \frac{V_0}{R} sin(2\pi \nu t)$ This expression comes from Ohm 's law: $V=IR$ .
Most common applications use a time-varying voltage source instead of a DC source. Examples include the commercial and residential power that serves so many of our needs.
Power dissipated by the AC circuit with a resistor in the example is: $P = \frac{V_0^2}{R} \cdot sin(2\pi \nu t)$ Therefore, average AC power is: $\frac{V_0^2}{2R}$ .

Term

Ohm's law
Ohm's observation is that the direct current flowing in an electrical circuit consisting only of resistances is directly proportional to the voltage applied.

Full Text

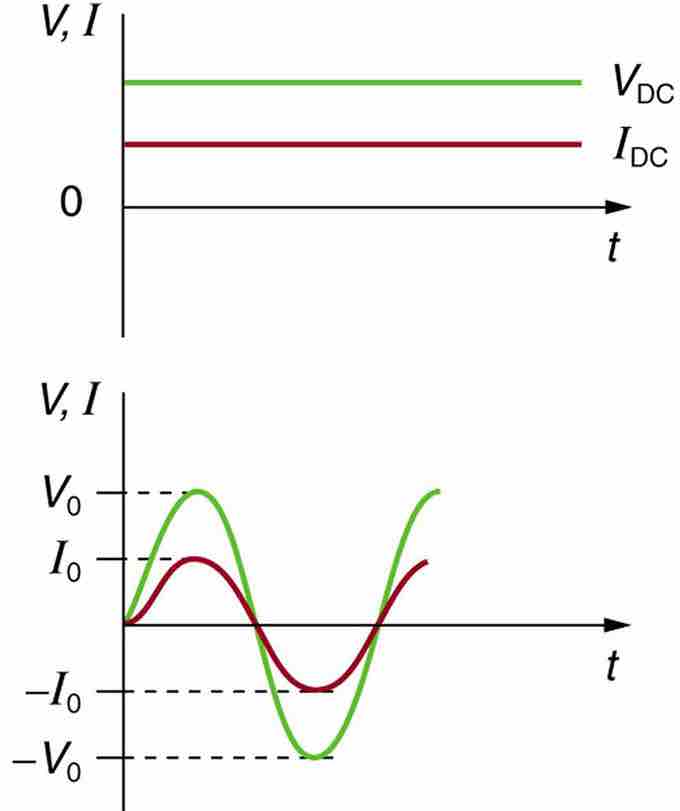
Direct current (DC) is the flow of electric charge in only one direction. It is the steady state of a constant-voltage circuit. Most well known applications, however, use a time-varying voltage source. Alternating current (AC) is the flow of electric charge that periodically reverses direction. If the source varies periodically, particularly sinusoidally, the circuit is known as an alternating-current circuit. Examples include the commercial and residential power that serves so many of our needs. shows graphs of voltage and current versus time for typical DC and AC power. The AC voltages and frequencies commonly used in homes and businesses vary around the world.

Sinusoidal Voltage and Current

(a) DC voltage and current are constant in time, once the current is established. (b) A graph of voltage and current versus time for 60-Hz AC power. The voltage and current are sinusoidal and are in phase for a simple resistance circuit. The frequencies and peak voltages of AC sources differ greatly.

We have studied Ohm's law:

$I = \frac{V}{R}$

where I is the current, V is the voltage, and R is the resistance of the circuit. Ohm's law applies to AC circuits as well as to DC circuits. Therefore, with an AC voltage given by:

$V = V_0 sin(2\pi \nu t)$

where V₀ is the peak voltage and $\nu$ is the frequency in hertz, the current in the circuit is given as:

$I = \frac{V_0}{R} sin(2\pi \nu t)$

In this example, in which we have a resistor and the voltage source in the circuit, the voltage and current are said to be in phase, as seen in (b). Current in the resistor alternates back and forth without any phase difference, just like the driving voltage.

Consider a perfect resistor that brightens and dims 120 times per second as the current repeatedly goes through zero. (A 120-Hz flicker is too rapid for your eyes to detect. ) The fact that the light output fluctuates means that the power is fluctuating. Since the power supplied is P = IV, if we use the above expressions for I and V, we see that the time dependence of power is:

$P = \frac{V_0^2}{R} \cdot sin(2\pi \nu t)$

To find the average power consumed by this circuit, we need to take the time average of the function. Since:

$\frac{1}{\pi}\int_{0}^{\pi}sin^2(x)dx = \frac{1}{2}$

we see that:

$P_{avg} = \frac{V_0^2}{2 R}$

[ edit ]

Prev Concept

RLC Series Circuit: At Large and Small Frequencies; Phasor Diagram

Capacitors in AC Circuits: Capacitive Reactance and Phasor Diagrams

Next Concept