Virtually all moving fluids exhibit viscosity, which is a measure of the resistance of a fluid to flow. Viscosity is a basic property necessary for the analysis of fluid flow.
Measure of Fluid Friction
It describes a fluid's internal resistance to movement and can be thought of as a measure of fluid friction. The greater the viscosity, the ‘thicker' the fluid and the more the fluid will resist movement.
Mathematically, viscosity is a proportionality constant relating an applied shear stress to the resulting shear velocity and is given, along with a representative diagram, (see ). As shown, when a force is applied to a fluid, creating a shear stress, the fluid will undergo a certain displacement. The viscosity of the fluid is then its inherent resistance to undergo this displacement.
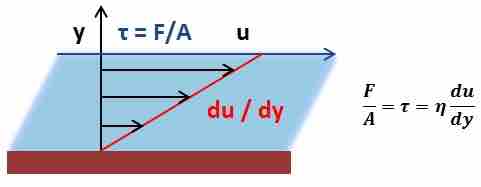
Representation of Viscosity
A proportionality constant relating an applied shear stress to the resulting shear velocity.
Different fluids exhibit different viscous behavior yet, in this analysis, only Newtonian fluids (fluids with constant velocity independent of applied shear stress) will be considered. Viscosity in fluids generally decreases with increasing temperature. The study of the viscous nature of fluids is called rheology.
In analyzing the properties of moving fluids, it is necessary to determine the nature of flow of the fluid. This is generally split into two categories, laminar and turbulent flow.
Turbulent Flow
Turbulent flow is characterized by irregular flow of a fluid in which there are both inconsistent flow patterns and velocity variations throughout the volume of the fluid in motion. Analysis of turbulent flow can be very complex and often requires advanced mathematical analysis to simulate flow in systems on a near case-by-case basis.
It occurs when the Reynolds number is above a certain critical threshold while mixed turbulent–laminar flow occurs within a range of Reynolds number below this threshold value. At the lower limit of this mixed turbulent–laminar flow Reynolds number region there is another critical threshold value, below which only laminar flow is possible.
Laminar Flow
Laminar flow consists of a regular-flow pattern with constant-flow velocity throughout the fluid volume and is much easier to analyze than turbulent flow.
Laminar flow is often encountered in common hydraulic systems, such as where fluid flow is through an enclosed, rigid pipe; the fluid is incompressible, has constant viscosity, and the Reynolds number is below this lower critical threshold value. It is characterized by the flow of a fluid in parallel layers, in which there is no disruption or interaction between the different layers, and in which each layer flows at a different velocity along the same direction. The variation in velocity between adjacent parallel layers is due to the viscosity of the fluid and resulting shear forces.
This figure (see ) gives a representation of the relative magnitudes of the velocity vectors of each of these layers for laminar fluid flow through a circular pipe, in a direction parallel to the pipe axis.
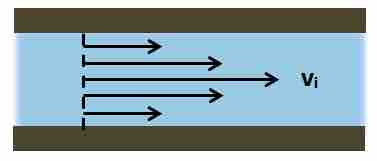
Relative Magnitudes of Velocity Vectors
Laminar fluid flow in a circular pipe at the same direction.
Considering laminar flow of a constant density, incompressible fluid such as for a Newtonian fluid traveling in a pipe, with a Reynolds number below the upper limit level for fully laminar flow, the pressure difference between two points along the pipe can be found from the volumetric flow rate, or vice versa. For such a system with a pipe radius of r, fluid viscosity η, distance between the two points along the pipe Δx = x2 – x1, and the volumetric flow rate Q, of the fluid, the pressure difference between the two points along the pipe Δp is given by Poiseuille's equation (see ).
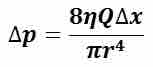
Poiseuille's Equation
Can be used to determine the pressure drop of a constant viscosity fluid exhibiting laminar flow through a rigid pipe.
This equation is valid for laminar flow of incompressible fluids only, and may be used to determine a number of properties in the hydraulic system, if the others are known or can be measured. In practice, Poiseuille's equation holds for most systems involving laminar flow of a fluid, except at regions where features disrupting laminar flow, such as at the ends of a pipe, are present.
Poiseuille's equation as given in this example (see ) is analogous to Ohm's equation for determining the resistance in an electronic circuit and is of great practical use in hydraulic-circuit analysis.
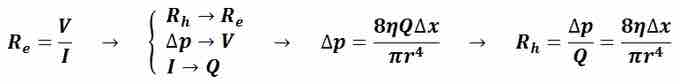
Poiseuille's Equation
Analogous to Ohm's Law Analogy