Blood flow is the continuous running of blood through vessels in the cardiovascular system (the mammalian cardiovascular system is shown in ). Blood is the viscous fluid composed of plasma and cells. The composition of the blood includes plasma, red blood cells, white blood cells and platelets. In microcirculation, the properties of the blood cells have an important influence on flow.
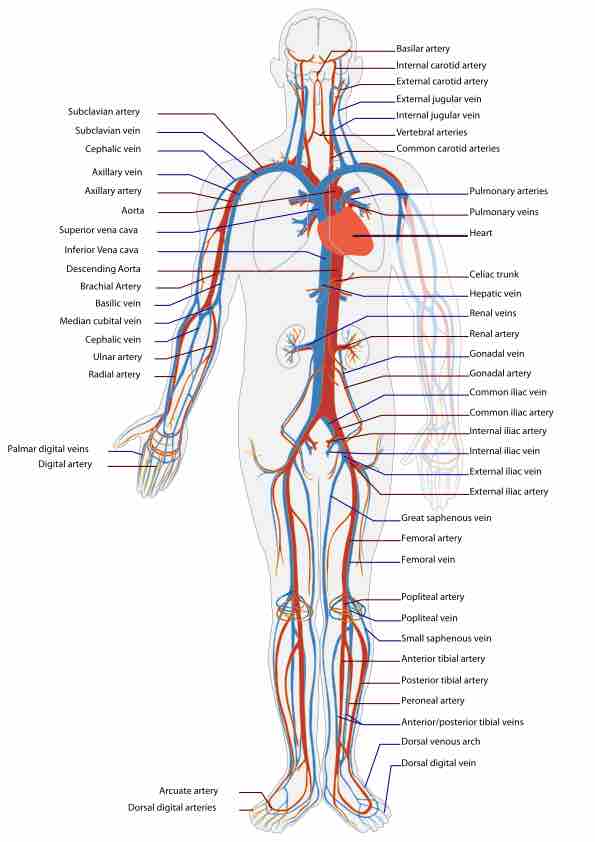
An illustrative overview of the mammalian cardiovascular system
Keep in mind that both circular paths are working simultaneously and not in a sequential manner as the numbering in the illustration might suggest. Both the ventricles are working together in harmony; as tiny amounts of blood are moving in the pulmonary circuit, the remainder of the blood moves through the systemic circuit.
The cardiovascular system, which consists of blood vessels and the heart, helps to distribute nutrients, O2, and other products of metabolism. The blood moves in the blood vessels, while the heart serves as the pump for the blood. The vessel walls of the heart are elastic and movable, therefore causing the blood and the wall to exert forces on each other and in turn influencing their respective motion.
The major quantity of interest in describing the motion of blood particles is velocity—the rate of change of the position of an object with time:
Blood velocities in arteries are higher during systole than during diastole. One parameter to quantify this difference is pulsatility index (PI), which is equal to the difference between the peak systolic velocity and the minimum diastolic velocity divided by the mean velocity during the cardiac cycle.
Another important parameter is the acceleration—the rate of change of velocity:
Normal plasma behaves like a Newtonian fluid at rates of shear. Typical values for the viscosity of normal human plasma at 37°C is 1.2Nsm-2. The viscosity of normal plasma varies with temperature in the same way as does that of its solvent, water. (a 5°C increase of temperature in the physiological range reduces plasma viscosity by about 10%).
The osmotic pressure of the plasma affects the mechanics of the circulation in several ways. An alteration of the osmotic pressure difference across the membrane of a blood cell causes a shift of water and a change in cell volume. The change, both in shape and flexibility, affects the mechanical properties of whole blood. Therefore, a change in plasma osmotic pressure alters the hematocrit (the volume concentration of red cells in the whole blood) by redistributing water between the intravascular and extravascular spaces. This in turn affects the mechanics of the whole blood.