Application of Bernoulli's Equation: Pressure and Speed

Application of Bernoulli's Equation

The relationship between pressure and velocity in ideal fluids is described quantitatively by Bernoulli's equation, named after its discoverer, the Swiss scientist Daniel Bernoulli (1700–1782). Bernoulli's equation states that for an incompressible and inviscid fluid, the total mechanical energy of the fluid is constant . (An inviscid fluid is assumed to be an ideal fluid with no viscosity. )

The total mechanical energy of a fluid exists in two forms: potential and kinetic. The kinetic energy of the fluid is stored in static pressure, $p_s$, and dynamic pressure, $\frac{1}{2}\rho V^2$, where \rho is the fluid density in (SI unit: kg/m³) and V is the fluid velocity (SI unit: m/s). The SI unit of static pressure and dynamic pressure is the pascal.

Static pressure is simply the pressure at a given point in the fluid, dynamic pressure is the kinetic energy per unit volume of a fluid particle. Thus, a fluid will not have dynamic pressure unless it is moving. Therefore, if there is no change in potential energy along a streamline, Bernoulli's equation implies that the total energy along that streamline is constant and is a balance between static and dynamic pressure. Mathematically, the previous statement implies:

$p_s + \frac{1}{2}\rho V^2 = constant$

along a streamline. If changes there are significant changes in height or if the fluid density is high, the change in potential energy should not be ignored and can be accounted for with,

$\Delta PE = \rho g \Delta h$.

This simply adds another term to the above version of the Bernoulli equation and results in

$p_s + \frac{1}{2}\rho V^2 + \rho g\Delta h = constant$.

Deriving Bernoulli's Equation

The Bernoulli equation can be derived by integrating Newton's 2nd law along a streamline with gravitational and pressure forces as the only forces acting on a fluid element. Given that any energy exchanges result from conservative forces, the total energy along a streamline is constant and is simply swapped between potential and kinetic.

Applying Bernoulli's Equation

Bernoulli's equation can be applied when syphoning fluid between two reservoirs . Another useful application of the Bernoulli equation is in the derivation of Torricelli's law for flow out of a sharp edged hole in a reservoir. A streamline can be drawn from the top of the reservoir, where the total energy is known, to the exit point where the static pressure and potential energy are known but the dynamic pressure (flow velocity out) is not.

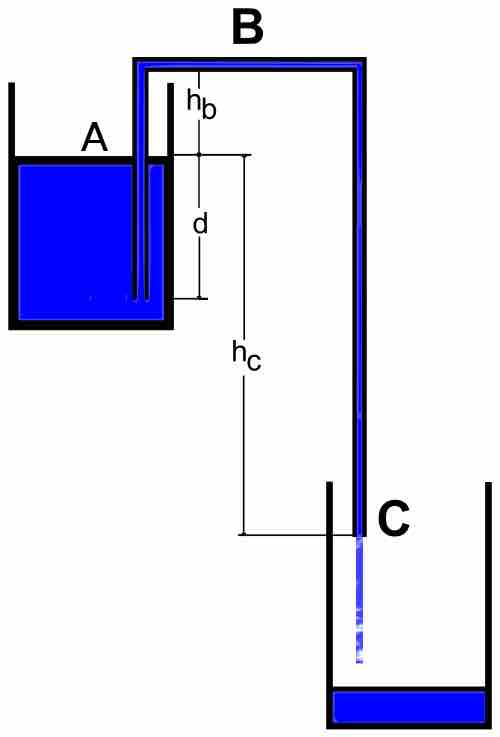
Syphoning

Syphoning fluid between two reservoirs. The flow rate out can be determined by drawing a streamline from point ( A ) to point ( C ).

Adapting Bernoulli's Equation

The Bernoulli equation can be adapted to flows that are both unsteady and compressible. However, the assumption of inviscid flow remains in both the unsteady and compressible versions of the equation. Compressibility effects depend on the speed of the flow relative to the speed of sound in the fluid. This is determined by the dimensionless quantity known as the Mach number. The Mach number represents the ratio of the speed of an object moving through a medium to the speed of sound in the medium.