Electric Potential Due to a Point Charge
Overview
Recall that the electric potential is defined as the electric potential energy per unit charge
The electric potential tells you how much potential energy a single point charge at a given location will have. The electric potential at a point is equal to the electric potential energy (measured in joules) of any charged particle at that location divided by the charge (measured in coulombs) of the particle. Since the charge of the test particle has been divided out, the electric potential is a "property" related only to the electric field itself and not the test particle. Another way of saying this is that because PE is dependent on q, the q in the above equation will cancel out, so V is not dependent on q.
The potential difference between two points ΔV is often called the voltage and is given by
Point Charges
Point charges, such as electrons, are among the fundamental building blocks of matter. Furthermore, spherical charge distributions (like on a metal sphere, see figure below) create external electric fields exactly like a point charge. The electric potential due to a point charge is, thus, a case we need to consider. Using calculus to find the work needed to move a test charge q from a large distance away to a distance of r from a point charge Q, and noting the connection between work and potential (W=–qΔV), it can be shown that the electric potential V of a point charge is
where k is a constant equal to 9.0×109 N⋅m2/C2 .
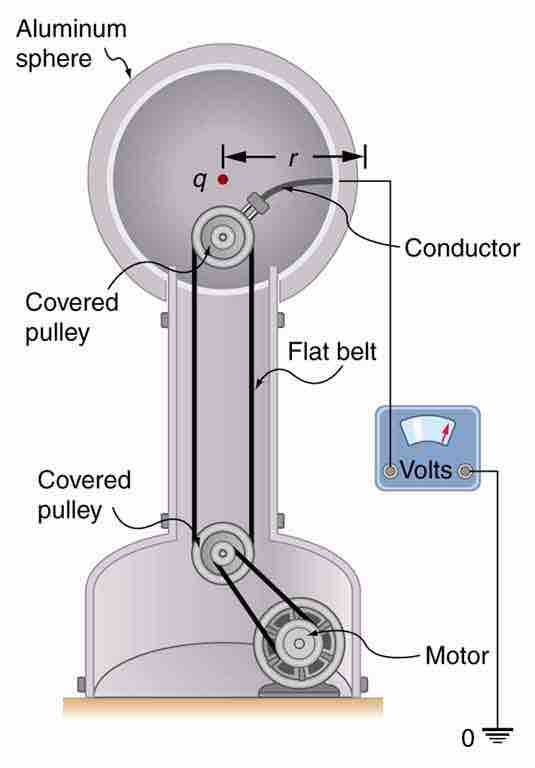
Van de Graaff Generator
The voltage of this demonstration Van de Graaff generator is measured between the charged sphere and ground. Earth's potential is taken to be zero as a reference. The potential of the charged conducting sphere is the same as that of an equal point charge at its center.
The potential at infinity is chosen to be zero. Thus V for a point charge decreases with distance, whereas E for a point charge decreases with distance squared:
The electric potential is a scalar while the electric field is a vector. Note the symmetry between electric potential and gravitational potential - both drop off as a function of distance to the first power, while both the electric and gravitational fields drop off as a function of distance to the second power.