Ideal Conductors

An ideal conductor is one that exists only in the world of theory. It is one that has certain "ideal" properties that make calculations of electric potential and field, and other properties simple to perform; it essentially eliminates the need for "corrections" to account for slight deviations from the so-called "ideal. " These ideal properties are:

σ = ∞

Conductivity (σ) is the inverse of resistance, measured in units of current per potential difference. In an ideal conductor, the material's conductivity is infinite, and its resistance approaches 0. This means that, ideally, it needs a minute amount of voltage (potential difference) to carry an extremely high amperage (current). The principle of near-zero resistance is akin to that of frictionless surfaces: tTheoretically, with the slightest force (voltage), an object (current) on a frictionless surface (zero-resistance conductor) can proceed without restriction.

E_tan = D_tan = 0

The electric field (E_tan) and electric flux density (D_tan) tangential to the surface of a conductor must be equal to 0. This is because any such field or flux that is tangential to the surface of the conductor must also exist inside the conductor, which by definition touches the tangential field or density at one point.

If an electric field exists inside the metal, there must be a drop in voltage between any two points along the surface of the metal. In a perfect conductor this drop should not exist because it implies a less-than-infinite conductivity.

D_n = _s

Electric flux density normal to the conductor's surface is equal to surface charge density. Essentially this means that the conductor's charge exists on its surface, not in its interior.

$\vec {E}_{int}=0$

This means that the electric field inside a perfect conductor is 0. The charges along the surface all act equally and opposite to one another, and their sum at any point is equal to 0.

ϕ_surface = constant

Charge distribution may vary depending on shape , but the potential over the surface of an ideal conductor is, at electrostatic equilibrium, constant throughout.

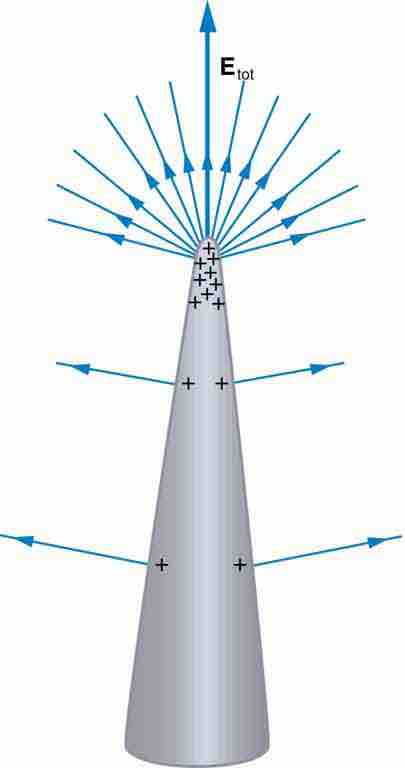
Charge Distribution on a Conductor with an Irregular Surface

Curvature causes electric field lines to extend such that they further distance themselves from one another with increasing distance from the conductor surface. As such, charges (and field lines) aggregate around areas of curvature.