In previous modules, we have seen puzzles from classical atomic theories (e.g., the Rutherford model). Most importantly, classical electrodynamics predicts that an atom described by a (classical) planetary model would be unstable. To explain the puzzle, Bohr proposed what is now called the Bohr model of the atom in 1913. He suggested that electrons could only have certain classical motions:
- Electrons in atoms orbit the nucleus.
- The electrons can only orbit stably, without radiating, in certain orbits (called by Bohr the "stationary orbits") at a certain discrete set of distances from the nucleus. These orbits are associated with definite energies and are also called energy shells or energy levels. In these orbits, the electron's acceleration does not result in radiation and energy loss as required by classical electrodynamics.
- Electrons can only gain and lose energy by jumping from one allowed orbit to another, absorbing or emitting electromagnetic radiation with a frequency
$\nu$ determined by the energy difference of the levels according to the Planck relation:$\Delta{E} = E_2-E_1=h\nu$ , where$h$ is the Planck constant. In addition, Bohr also assumed that the angular momentum$L$ is restricted to be an integer multiple of a fixed unit:$L = n{h \over 2\pi} = n\hbar$ , where$n = 1, 2, 3, \dots$ is called the principal quantum number, and$\hbar = \frac{h}{2\pi}$ .
We have seen that Planck adopted a new condition of energy quantization to explain the black body radiation, where he introduced the Planck constant
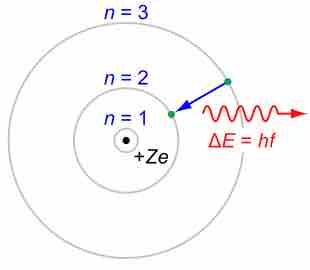
Rutherford-Bohr model
The Rutherford–Bohr model of the hydrogen atom (