Diffusion
The kinetic theory describes a gas as a large number of submicroscopic particles (atoms or molecules), all of which are in constant rapid motion that has randomness arising from their many collisions with each other and with the walls of the container.
Diffusion refers to the process of particles moving from an area of high concentration to one of low concentration. The rate of this movement is a function of temperature, viscosity of the medium, and the size (mass) of the particles. Diffusion results in the gradual mixing of materials, and eventually, it forms a homogeneous mixture.
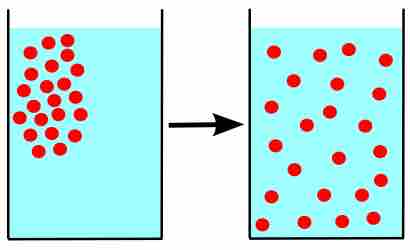
Diffusion
Particles in a liquid-filled beaker are initially concentrated in one area, but diffuse from their area of high concentration to the areas of low concentration until they are distributed evenly throughout the liquid.
Effusion
Not only do gaseous particles move with high kinetic energy, but their small size enables them to move through small openings as well; this process is known as effusion. For effusion to occur, the hole's diameter must be smaller than the molecules' mean free path (the average distance that a gas particle travels between successive collisions with other gas particles). The opening of the hole must be smaller than the mean free path because otherwise, the gas could move back and forth through the hole.
Effusion is explained by the continuous random motion of particles; over time, this random motion guarantees that some particles will eventually pass through the hole.
Graham's Law
Scottish chemist Thomas Graham experimentally determined that the ratio of the rates of effusion for two gases is equal to the square root of the inverse ratio of the gases' molar masses. This is written as follows:
where M represents the molar mass of the molecules of each of the two gases.
The gases' effusion rate is directly proportional to the average velocity at which they move; a gas is more likely to pass through an orifice if its particles are moving at faster speeds.
Example
What is the ratio of the rate of effusion of ammonia, NH3, to that of hydrogen chloride, HCl?
The NH3 molecules effuse at a rate 1.46 times faster than HCl molecules.
Derivation of Graham's Law
Graham's Law can be understood as a consequence of the average molecular kinetic energy of two different gas molecules (marked 1 and 2) being equal at the same temperature. (Recall that a result of the Kinetic Theory of Gases is that the temperature, in degrees Kelvin, is directly proportional to the average kinetic energy of the molecules.) Therefore, equating the kinetic energy of molecules 1 and 2, we obtain:
The rate of effusion is determined by the number of molecules that diffuse through the hole in a unit of time, and therefore by the average molecular velocity of the gas molecules.