Concentration of Cells

Gibbs Free Energy and Cell Potential

The standard potential of an electrochemical cell requires standard conditions for all of the reactants. When reactant concentrations differ from standard conditions, the cell potential will deviate from the standard potential. In the late 19th century, Josiah Willard Gibbs formulated a theory to predict whether a chemical reaction would be spontaneous based on free energy:

$\Delta G = \Delta G^o + RT \times ln\ Q$

Here, ΔG is the change in Gibbs free energy, T is absolute temperature, R is the gas constant, and Q is the reaction quotient. In chemistry, a reaction quotient is a function of the activities or concentrations of the chemical species involved in a chemical reaction. Gibbs' key contribution was to formalize the understanding of the effect of reactant concentration on spontaneity.

In the 20th century, German chemist Walther Nernst extended Gibbs' theory to include the contribution from electric potential on charged species. The change in Gibbs free energy for an electrochemical cell can be related to the cell potential. Therefore, Gibbs' theory is:

$nF\Delta E = nF\Delta E^o - RT\times ln\ Q$

Here, n is the number of moles of electrons, F is the Faraday constant ($\frac {Coulombs}{mole}$), and ΔE is the cell potential.

Walther Nernst

A portrait of Walther Nernst

The Nernst Equation

Finally, Nernst divided by the amount of charge transferred to arrive at a new equation that now bears his name. The Nernst equation is:

$\Delta E = \Delta E^o - \frac{RT}{nF} \times ln\ Q$

The Nernst equation can be used to calculate the output voltage changes in a pair of half-cells under non-standard conditions.

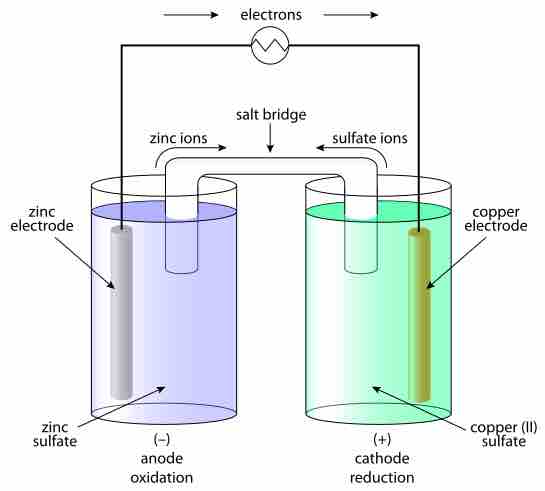
A typical galvanic electrochemical cell

Under standard conditions, the output of this pair of half-cells is well known. When a change in the concentration or activity of reactants occurs, or the temperature or pressure changes, the output voltage changes. It is calculated via the Nernst equation.