A base is a substance that decreases the hydrogen ion (H+) concentration of a solution. In the more generalized Brønsted-Lowry definition, the hydroxide ion (OH-) is the base because it is the substance that combines with the proton. Ammonia and some organic nitrogen compounds can combine with protons in solution and act as Brønsted-Lowry bases. These compounds are generally weaker bases than the hydroxide ion because they have less attraction for protons. For example, when ammonia competes with OH- for protons in an aqueous solution, it is only partially successful. It can combine with only a portion of the H+ ions, so it will have a measurable equilibrium constant. Reactions with weak bases result in a relatively low pH compared to strong bases. Bases range from a pH of greater than 7 (7 is neutral like pure water) to 14 (though some bases are greater than 14).
An alkaline buffer can be made from a mixture of a base and its conjugate acid, similar to the way in which weak acids and their conjugate bases can be used to make a buffer.
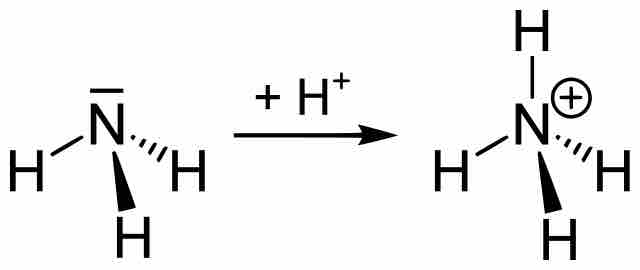
Ammonia to ammonium ion
Two-dimensional image depicting the association of proton (H+) with the weak base ammonia (NH3) to form its conjugate acid, ammonium ion (NH4+).
Calculating the pH of a Base
The pH of bases is usually calculated using the OH- concentration to find the pOH first. This is done because the H+ concentration is not a part of the reaction, while the OH- concentration is. The formula for pOH is:
By multiplying a conjugate acid (such as NH4+) and a conjugate base (such as NH3) the following is given:
The pH can be calculated using the formula:
Weak bases exist in chemical equilibrium much in the same way as weak acids do. A base dissociation constant (Kb) indicates the strength of the base. For example, when ammonia is put in water, the following equilibrium is set up:
Bases that have a large Kb will ionize more completely, meaning they are stronger bases. NaOH (sodium hydroxide) is a stronger base than (CH3CH2)2NH (diethylamine) which is a stronger base than NH3 (ammonia). As the bases get weaker, the Kb values get smaller.
Example:
Calculate the pH of a buffer solution consisting of 0.051 M NH3 and 0.037 M NH4+. The Kb for NH3 = 1.8 x 10-5.
Assuming the change (x) is negligible to 0.051 M and 0.037 M solutions:
1.8 x 10-5
x = [OH-] = 2.48 x 10-5
pOH = 4.61
pH = 14 - 4.61 = 9.39