Numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and, by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of definite integrals. The term numerical quadrature (often abbreviated to quadrature) is more or less a synonym for numerical integration, especially as applied to one-dimensional integrals. Numerical integration over more than one dimension is sometimes described as cubature, although the meaning of quadrature is understood for higher dimensional integration as well.
The basic problem considered by numerical integration is to compute an approximate solution to a definite integral:
If
Reasons for numerical integration
- There are several reasons for carrying out numerical integration. The integrand
$f(x)$ may be known only at certain points, such as when obtained by sampling. Some embedded systems and other computer applications may need numerical integration for this reason. - A formula for the integrand may be known, but it may be difficult or impossible to find an antiderivative which is an elementary function. An example of such an integrand
$f(x)=\exp(-x^2)$ , the antiderivative of which (the error function, times a constant) cannot be written in elementary form. - It may be possible to find an antiderivative symbolically, but it may be easier to compute a numerical approximation than to compute the antiderivative. That may be the case if the antiderivative is given as an infinite series or product, or if its evaluation requires a special function which is not available.
Methods for One-Dimensional Integrals
A large class of quadrature rules can be derived by constructing interpolating functions which are easy to integrate. Typically these interpolating functions are polynomials. The simplest method of this type is to let the interpolating function be a constant function (a polynomial of degree zero) which passes through the point
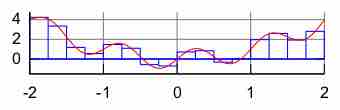
Rectangle Rule
Illustration of the rectangle rule.
The interpolating function may be an affine function (a polynomial of degree 1) which passes through the points
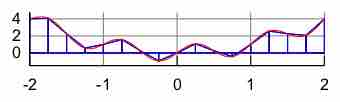
Trapezoidal Rule
Illustration of the trapezoidal rule.
For either one of these rules, we can make a more accurate approximation by breaking up the interval
where the subintervals have the form