Improper Integrals

An improper integral is the limit of a definite integral as an endpoint of the interval(s) of integration approaches either a specified real number or $\infty$ or $-\infty$ or, in some cases, as both endpoints approach limits. Such an integral is often written symbolically just like a standard definite integral, perhaps with infinity as a limit of integration. But that conceals the limiting process.

Specifically, an improper integral is a limit of one of two forms.

First, an improper integral could be a limit of the form:

$\displaystyle \lim_{b\to\infty} \int_a^bf(x)\, \mathrm{d}x, \, \lim_{a\to -\infty} \int_a^bf(x)\, \mathrm{d}x$

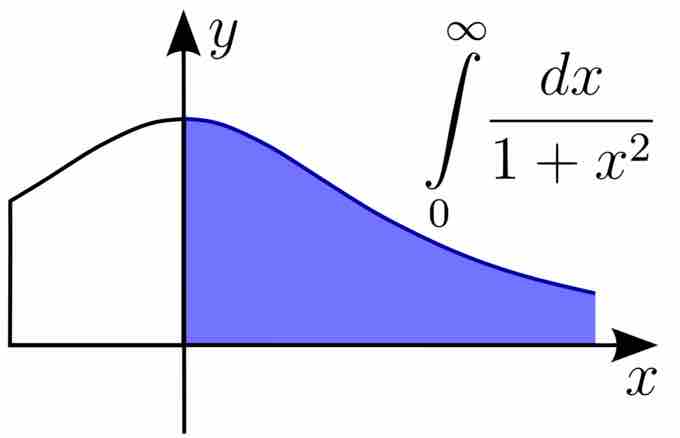
Improper Integral of the First Kind

The integral may need to be defined on an unbounded domain.

Second, an improper integral could be a limit of the form:

$\displaystyle \lim_{c\to b^-} \int_a^cf(x)\, \mathrm{d}y,\, \lim_{c\to a^+} \int_c^bf(x)\, \mathrm{d}x$

in which one takes a limit at one endpoint or the other (or sometimes both). 

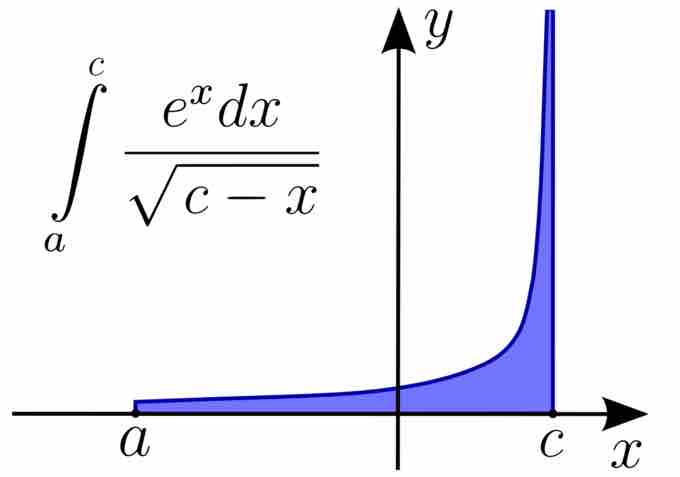
Improper Integral of the Second Kind

An improper Riemann integral of the second kind.The integral may fail to exist because of a vertical asymptote in the function.

Integrals are also improper if the integrand is undefined at an interior point of the domain of integration, or at multiple such points. It is often necessary to use improper integrals in order to compute a value for integrals which may not exist in the conventional sense (as a Riemann integral, for instance) because of a singularity in the function, or an infinite endpoint of the domain of integration.

Example 1

The original definition of the Riemann integral does not apply to a function such as $\frac{1}{x^2}$ on the interval $[1, \infty]$, because in this case the domain of integration is unbounded. However, the Riemann integral can often be extended by continuity, by defining the improper integral instead as a limit:

$\begin{aligned} \int_1^\infty \frac{1}{x^2}\,\mathrm{d}x &=\lim_{b\to\infty} \int_1^b\frac{1}{x^2}\,\mathrm{d}x \\ &= \lim_{b\to\infty} \left(-\frac{1}{b} + \frac{1}{1}\right) \\ &= 1\end{aligned}$

Example 2

The narrow definition of the Riemann integral also does not cover the function $\frac{1}{\sqrt{x}}$ on the interval $[0, 1]$. The problem here is that the integrand is unbounded in the domain of integration (the definition requires that both the domain of integration and the integrand be bounded). However, the improper integral does exist if understood as the limit

$\begin{aligned}\displaystyle \int_0^1 \frac{1}{\sqrt{x}}\,\mathrm{d}x &=\lim_{a\to 0^+}\int_a^1\frac{1}{\sqrt{x}}\, \mathrm{d}x \\ &= \lim_{a\to 0^+}(2\sqrt{1}-2\sqrt{a})\\ &=2\end{aligned}$