Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods have been used for specific curves. The advent of infinitesimal calculus led to a general formula, which we will learn in this atom. We will also use integration to calculate the surface area of a three-dimensional object.
Arc Length
Consider a real function
Consider an infinitesimal part of the curve
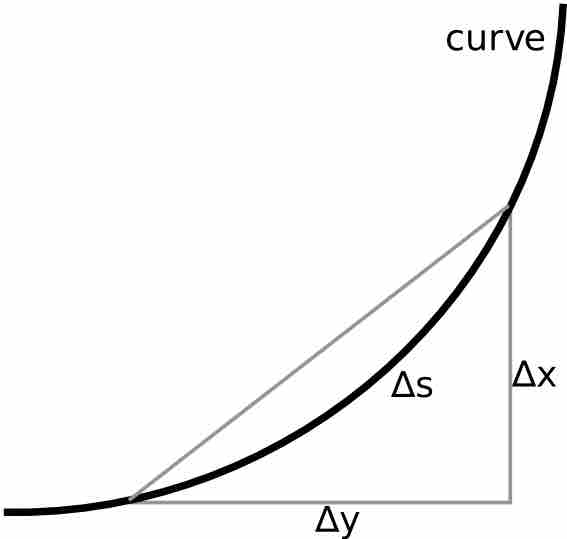
Approximating Deltas
For a small piece of curve,
If a curve is defined parametrically by
This is more clearly a consequence of the distance formula, where instead of a
Surface Area
For rotations around the
Example
For a circle
The curve can be represented parametrically as
Now, calculate the surface area of the solid obtained by rotating