Integration is commonly used in statistical analysis, especially when a random variable takes a continuum value. Here, we will learn what probability distribution function is and how it functions with regard to integration.
In probability theory, a probability density function (pdf), or density of a continuous random variable, is a function that describes the relative likelihood for this random variable to take on a given value. The probability for the random variable to fall within a particular region is given by the integral of this variable's probability density over the region. The probability density function is nonnegative everywhere, and its integral over the entire space is equal to one.
Probability Density Function
A probability density function is most commonly associated with absolutely continuous univariate distributions.
For a continuous random variable
where
The integral of the pdf in the range
The expected value of
Example: Normal Distribution
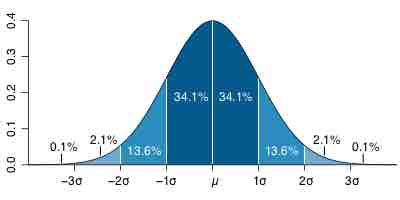
Probability Distribution Function
Probability distribution function of a normal (or Gaussian) distribution, where mean
The standard normal distribution has probability density
This probability distribution has the mean and variance, denoted by