Calculus, in general, has a broad applications in diverse fields of science, finance, and business. In this atom, we will see some examples of applications of integration in economics and biology.
Consumer Surplus
In mainstream economics, economic surplus (also known as total welfare or Marshallian surplus) refers to two related quantities. Consumer surplus is the monetary gain obtained by consumers; they are able to buy something for less than they had planned on spending. Producer surplus is the amount that producers benefit from selling at a market price that is higher than their lowest price, thereby making more profit .
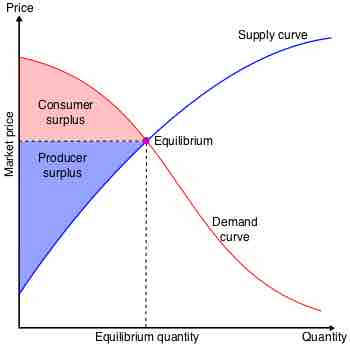
Supply and Demand Chart
Graph illustrating consumer (red) and producer (blue) surpluses on a supply and demand chart.
In calculus terms, consumer surplus is the derivative of the definite integral of the demand function with respect to price, from the market price to the maximum reservation price—i.e. the price-intercept of the demand function:
where
Blood Flow
The human body is made up of several processes, all carrying out various functions, one of which is the continuous running of blood in the cardiovascular system. If we wanted, we could obtain a general expression for the volume of blood across a cross section per unit time (a quantity called flux). Since we can assume that there is a cylindrical symmetry in the blood vessel, we first consider the volume of blood passing through a ring with inner radius
where
where
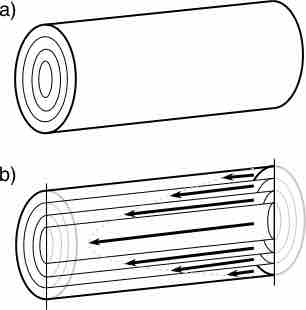
Blood Flow
(a) A tube; (b) The blood flow close to the edge of the tube is slower than that near the center.