Physics and Engeineering: Center of Mass

Center of Mass

In physics, the center of mass (COM) of a mass or object in space is the unique point at which the weighted relative position of the distributed mass sums to zero. In this case, the distribution of mass is balanced around the center of mass and the average of the weighted position coordinates of the distributed mass defines its coordinates. Calculations in mechanics are simplified when formulated with respect to the COM.

System of Particles

In the case of a system of particles $P_i, i = 1, \cdots, n$, each with a mass, $m_i$_, which are located in space with coordinates $r_i, i = 1, \cdots, n$, the coordinates $\mathbf{R}$ of the center of mass satisfy the following condition: 

$\displaystyle{\sum_{i=1}^n m_i(\mathbf{r}_i - \mathbf{R}) = 0}$

Solve this equation for $\mathbf{R}$ to obtain the formula 

$\displaystyle{\mathbf{R} = \frac{1}{M} \sum_{i=1}^n m_i \mathbf{r}_i}$

where $M$ is the sum of the masses of all of the particles.

Continuous Distribution

If the mass distribution is continuous with respect to the density, $\rho (r)$, within a volume, $V$, then the integral of the weighted position coordinates of the points in this volume relative to the center of mass, $\mathbf{R}$, is zero, that is: 

$\displaystyle{\int_V \rho(\mathbf{r})(\mathbf{r}-\mathbf{R})dV = 0}$

Solve this equation for the coordinates $\mathbf{R}$ to obtain: 

$\displaystyle{\mathbf R = \frac 1M \int_V\rho(\mathbf{r}) \mathbf{r} dV}$ 

where $M$ is the total mass in the volume. If a continuous mass distribution has uniform density, which means $\rho$ is constant, then the center of mass is the same as the centroid of the volume.

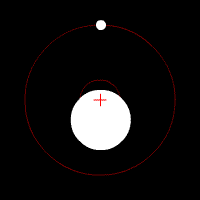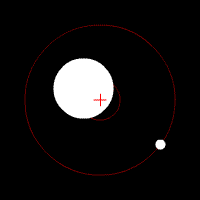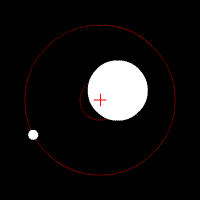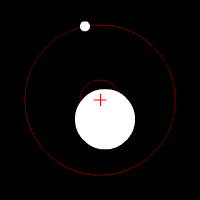
Two Bodies and the COM

Two bodies orbiting the COM located inside one body. COM can be defined for both discrete and continuous systems. The two objects are rotating around their center of mass.