Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point. The Taylor series of a real or complex-valued function
where
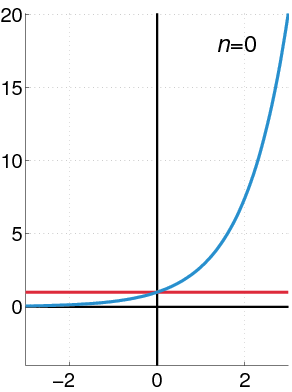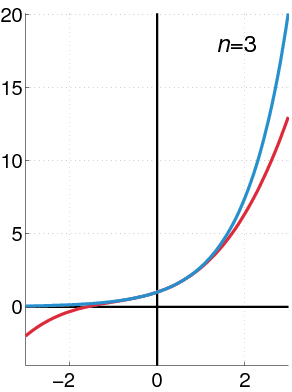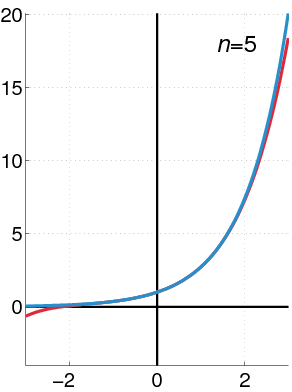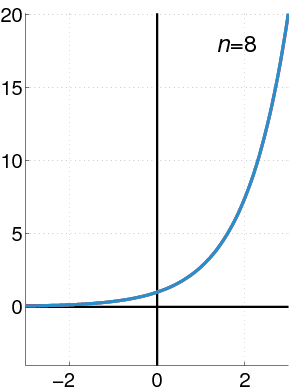
Exponential Function as a Taylor Series
The exponential function (in blue) and the sum of the first 9 terms of its Taylor series at 0 (in red).
Example
The Taylor series for the exponential function
Using Taylor Series to Evaluate an Integral
Taylor series can be used to evaluate an integral when there is no other integration technique available (of course, other than numerical integration). Let's assume that the integration of a function (
Therefore, as long as Taylor expansion is possible and the infinite sum converges, the definite integral (